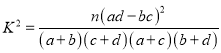题目内容
【题目】某大学艺术专业400名学生参加某次测评,根据男女学生人数比例,使用分层抽样的方法从中随机抽取了100名学生,记录他们的分数,将数据分成7组:![]() ,
,![]() ,…,
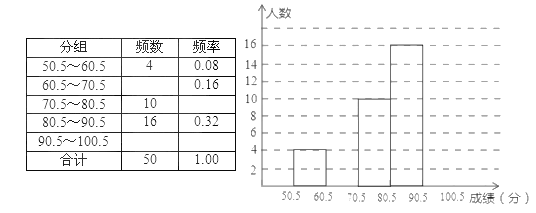
,…,![]() ,并整理得到如下频率分布直方图:
,并整理得到如下频率分布直方图:

(1)从总体的400名学生中随机抽取一人,估计其分数小于70的概率;
(2)已知样本中分数小于40的学生有5人,试估计总体中分数在区间![]() 内的人数;
内的人数;
(3)已知样本中有一半男生的分数不小于70,且样本中分数不小于70的男女生人数相等,试估计总体中男生和女生人数的比例.
【答案】(1) ![]() ;(2) 20;(3)
;(2) 20;(3) ![]() .
.
【解析】试题分析:(Ⅰ)根据频率=组距×高,可得分数小于70的概率为:1﹣(0.04+0.02)×10;(Ⅱ)先计算样本中分数小于40的频率,进而计算分数在区间[40,50)内的频率,可估计总体中分数在区间[40,50)内的人数;
(Ⅲ)已知样本中有一半男生的分数不小于70,且样本中分数不小于70的男女生人数相等.进而得到答案.
试题解析:
(1)由频率分布直方图知,
分数在![]() 的频率为
的频率为![]() ,
,
分数在![]() 的频率为
的频率为![]() ,
,
则分数小于70的频率为![]() ,
,
故从总体的400名学生中随机抽取一人,估计其分数小于70的概率为![]() .
.
(2)由频率分布直方图知,
样本中分数在区间![]() 的人数为
的人数为![]() (人),
(人),
已知样本中分数小于40的学生有5人,
所以样本中分数在区间![]() 内的人数为
内的人数为![]() (人),
(人),
设总体中分数在区间![]() 内的人数为
内的人数为![]() ,
,
则![]() ,得
,得![]() ,
,
所以总体中分数在区间![]() 内的人数为20人.
内的人数为20人.
(3)由频率分布直方图知,
分数不小于70的人数为![]() (人),
(人),
已知分数不小于70的男女生人数相等,
故分数不小于70分的男生人数为30人,
又因为样本中有一半男生的分数不小于70,
故男生的频率为:![]() ,
,
即女生的频率为:![]() ,
,
即总体中男生和女生人数的比例约为:![]() .
.

 智慧小复习系列答案
智慧小复习系列答案【题目】为了研究某种微生物的生长规律,需要了解环境温度![]() (
(![]() )对该微生物的活性指标
)对该微生物的活性指标![]() 的影响,某实验小组设计了一组实验,并得到如表的实验数据:
的影响,某实验小组设计了一组实验,并得到如表的实验数据:
环境温度 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
活性指标 |
|
|
|
|
|
|
|
(Ⅰ)由表中数据判断![]() 关于
关于![]() 的关系较符合
的关系较符合![]() 还是
还是![]() ,并求
,并求![]() 关于
关于![]() 的回归方程(
的回归方程(![]() ,
,![]() 取整数);
取整数);
(Ⅱ)根据(Ⅰ)中的结果分析:若要求该种微生物的活性指标不能低于![]() ,则环境温度应不得高于多少
,则环境温度应不得高于多少![]() ?
?
附: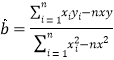 ,
,![]()