题目内容
如图四棱锥E—ABCD中,底面ABCD是平行四边形。∠ABC=45°,BE=BC= EA=EC=6,M为EC中点,平面BCE⊥平面ACE,AE⊥EB
EA=EC=6,M为EC中点,平面BCE⊥平面ACE,AE⊥EB

(I)求证:AE⊥BC (II)求四棱锥E—ABCD体积
 EA=EC=6,M为EC中点,平面BCE⊥平面ACE,AE⊥EB
EA=EC=6,M为EC中点,平面BCE⊥平面ACE,AE⊥EB
(I)求证:AE⊥BC (II)求四棱锥E—ABCD体积
(1)根据题意,由于BM⊥平面ACE, AE⊥BM,那么可以根据线面垂直的性质定理得到证明。
(2)
(2)

试题分析:(1)证明:BE=BC, M为EC中点 ∴BM⊥EC
又平面BCE⊥平面ACE 且交于EC
∴BM⊥平面ACE, AE⊥BM
又AE⊥EB EB
 BM=B BM、EB
BM=B BM、EB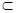 平面BCE
平面BCE∴AE⊥平面BCE, AE⊥BC
(2)设E点到平面ABCD距离为








点评:主要是考查了空间中线面位置关系,以及锥体体积的计算,属于中档题。

练习册系列答案
 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目
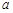 、
、 是两条不同的直线,
是两条不同的直线, 、
、 是两个不同的平面,是下列命题中正确的是( )
是两个不同的平面,是下列命题中正确的是( ) ,
, ,则
,则
 ,
,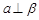
 ,
, ,
, ,则
,则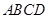 中,
中,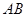 ,
,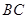 ,
,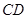 两两互相垂直,且
两两互相垂直,且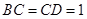 .
.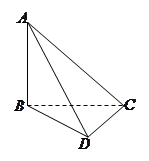
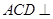 平面
平面 ;
;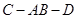 的大小;
的大小;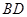 与平面
与平面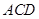 所成的角为
所成的角为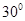 ,求线段
,求线段
 中,
中, 分别是棱
分别是棱 的中点,则异面直线
的中点,则异面直线 与
与 所成的角等于__________.
所成的角等于__________.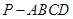 中,侧棱都相等,底面是边长为
中,侧棱都相等,底面是边长为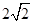 的正方形,底面中心为
的正方形,底面中心为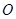 ,以
,以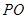 为直径的球经过侧棱中点,则该球的体积为( )
为直径的球经过侧棱中点,则该球的体积为( )
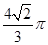


 的正方形E, F分别为PC,BD的中点,侧面PAD⊥底面ABCD,且PA=PD=
的正方形E, F分别为PC,BD的中点,侧面PAD⊥底面ABCD,且PA=PD= AD.
AD.
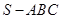 中,侧面
中,侧面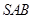 与侧面
与侧面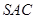 均为等边三角形,
均为等边三角形, 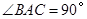 ,
,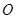 为
为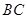 中点.
中点.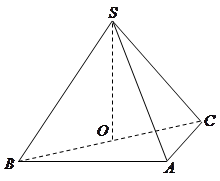
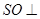 平面
平面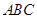 ;
;