题目内容
【题目】已知函数f(x)=alnx+x2(a为实常数).
(Ⅰ)若a=﹣2,求证:函数f(x)在(1,+∞)上是增函数;
(Ⅱ)求函数f(x)在[1,e]上的最小值及相应的x值.
【答案】解:(Ⅰ)当a=﹣2时,f(x)=x2﹣2lnx,当x∈(1,+∞), ![]() ,
,
故函数f(x)在(1,+∞)上是增函数.
(Ⅱ) ![]() ,当x∈[1,e],2x2+a∈[a+2,a+2e2].
,当x∈[1,e],2x2+a∈[a+2,a+2e2].
若a≥﹣2,f'(x)在[1,e]上非负(仅当a=﹣2,x=1时,f'(x)=0),
故函数f(x)在[1,e]上是增函数,此时[f(x)]min=f(1)=1.
若﹣2e2<a<﹣2,当 ![]() 时,f'(x)=0;当
时,f'(x)=0;当 ![]() 时,f'(x)<0,
时,f'(x)<0,
此时f(x)是减函数;当 ![]() 时,f'(x)>0,此时f(x)是增函数.
时,f'(x)>0,此时f(x)是增函数.
故[f(x)]min= 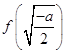 =
= ![]()
若a≤﹣2e2,f'(x)在[1,e]上非正(仅当a=﹣2e2,x=e时,f'(x)=0),
故函数f(x)在[1,e]上是减函数,此时[f(x)]min=f(e)=a+e2.
综上可知,当a≥﹣2时,f(x)的最小值为1,相应的x值为1;
当﹣2e2<a<﹣2时,f(x)的最小值为 ![]() ,相应的x值为
,相应的x值为 ![]() ;
;
当a≤﹣2e2时,f(x)的最小值为a+e2,相应的x值为e
【解析】(Ⅰ)将a=﹣2代入,然后求出导函数f'(x),欲证函数f(x)在(1,+∞)上是增函数只需证导函数在(1,+∞)上恒大于零即可;(Ⅱ)先求出导函数f'(x),然后讨论a研究函数在[1,e]上的单调性,将f(x)的各极值与其端点的函数值比较,其中最小的一个就是最小值.
【考点精析】掌握利用导数研究函数的单调性和函数的最大(小)值与导数是解答本题的根本,需要知道一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值.
比较,其中最大的是一个最大值,最小的是最小值.

【题目】某工程设备租赁公司为了调查A,B两种挖掘机的出租情况,现随机抽取了这两种挖掘机各100台,分别统计了每台挖掘机在一个星期内的出租天数,统计数据如下表: A型车挖掘机
出租天数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
车辆数 | 5 | 10 | 30 | 35 | 15 | 3 | 2 |
B型车挖掘机
出租天数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
车辆数 | 14 | 20 | 20 | 16 | 15 | 10 | 5 |
(Ⅰ)根据这个星期的统计数据,将频率视为概率,求该公司一台A型挖掘机,一台B型挖掘机一周内合计出租天数恰好为4天的概率;
(Ⅱ)如果A,B两种挖掘机每台每天出租获得的利润相同,该公司需要从A,B两种挖掘机中购买一台,请你根据所学的统计知识,给出建议应该购买哪一种类型,并说明你的理由.