题目内容
设数列{an}.
A.若 =4n,n∈N*,则{an}为等比数列 =4n,n∈N*,则{an}为等比数列 |
B.若an an+2= an+2=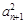 ,n∈N*,则{an}为等比数列 ,n∈N*,则{an}为等比数列 |
C.若am an=2m+n,m,n∈N*,则{an}为等比数列 an=2m+n,m,n∈N*,则{an}为等比数列 |
D.若an an+3=an+1 an+3=an+1 an+2,n∈N*,则{an}为等比数列 an+2,n∈N*,则{an}为等比数列 |
C
解析试题分析:利用等比数列的概念,通过特例法对A,B,C,D四个选项逐一判断排除即可.A中,
 例如
例如 不是等比数列,故A错;B中,若
不是等比数列,故A错;B中,若 满足
满足 ,但
,但 不是等比数列,故B错,
不是等比数列,故B错,
同理也排除D;
对于C,

 为等比数列,故C正确.
为等比数列,故C正确.
考点:等比数列的性质;等差数列的性质.
点评:本题考查等比数列的概念与性质,考查举例排除法的应用,考查分析问题与解决问题的能力,属于中档题.

练习册系列答案
 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
若{an}是等比数列,且an>0,a2a4+2a3a5+a4a6=25,则a3+a5的值为
| A.5 | B.10 | C.15 | D.20 |
已知a,b,a+b成等差数列,a,b,ab成等比数列,且0<log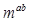 <1,则m的取值范围是( )
<1,则m的取值范围是( )
| A.m>1 | B.1<m<8 |
| C.m>8 | D.0<m<1或m>8 |
若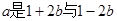 的等比中项,则
的等比中项,则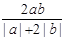 的最大值为( )
的最大值为( )
A.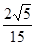 | B.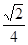 | C.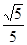 | D.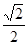 |
已知函数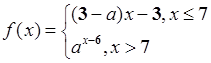 ,若数列
,若数列 满足
满足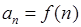 (
(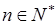 ),且
),且 是递增数列,则实数
是递增数列,则实数 的取值范围是( )
的取值范围是( )
A.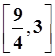 | B.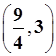 | C.(2,3) | D.(1,3) |
已知点 (
( ,
, )(
)( N*)都在函数
N*)都在函数 (
( )的图象上,则
)的图象上,则 与
与 的大小关系是( )
的大小关系是( )
A. > > | B. < < |
C. = = | D. 与 与 的大小与 的大小与 有关 有关 |
设 ,
,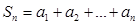 ,在
,在 中,正数的个数是( )
中,正数的个数是( )
| A.25 | B.50 | C.75 | D.100 |
若四个正数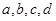 成等差数列,
成等差数列,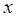 是
是 和
和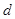 的等差中项,
的等差中项, 是
是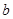 和
和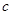 的等比中项,则
的等比中项,则 和
和 的大小关系是
的大小关系是
A.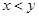 | B.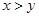 | C.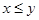 | D.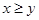 |
已知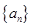 是等比数列,
是等比数列,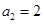 ,
,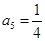 ,则
,则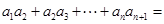 ( )
( )
A.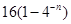 | B.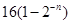 | C.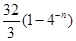 | D.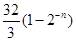 |