题目内容
若四个正数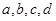 成等差数列,
成等差数列,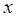 是
是 和
和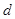 的等差中项,
的等差中项, 是
是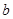 和
和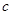 的等比中项,则
的等比中项,则 和
和 的大小关系是
的大小关系是
A.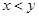 | B.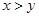 | C.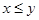 | D.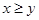 |
D
解析试题分析:依题意可知2x=a+d,y=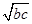 ,∵
,∵ ,又因为四个正数
,又因为四个正数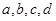 成等差数列,则可知a+d=b+c,代入可知得到x≥y,故选D
成等差数列,则可知a+d=b+c,代入可知得到x≥y,故选D
考点:本题主要考查查了等比数列和等差数列的性质.考查了学生对等比数列和等差数列基础知识的掌握
点评:解决该试题的关键是先根据题意知2x=a+d,y=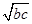 ,根据等差中项的性质可知a+d=b+c,根据基本不等式性质可知
,根据等差中项的性质可知a+d=b+c,根据基本不等式性质可知 进而求得答案.
进而求得答案.

练习册系列答案
 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
等比数列{an}中,a2=9,a5=243,则{an}的前4项和为( ).
| A.81 | B.120 | C.168 | D.192 |
设数列{an}.
A.若 =4n,n∈N*,则{an}为等比数列 =4n,n∈N*,则{an}为等比数列 |
B.若an an+2= an+2=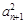 ,n∈N*,则{an}为等比数列 ,n∈N*,则{an}为等比数列 |
C.若am an=2m+n,m,n∈N*,则{an}为等比数列 an=2m+n,m,n∈N*,则{an}为等比数列 |
D.若an an+3=an+1 an+3=an+1 an+2,n∈N*,则{an}为等比数列 an+2,n∈N*,则{an}为等比数列 |
三个数成等比数列,其和为14,各数平方和为84,则这三个数为( )
| A.2,4,8 | B.8,4,2 |
| C.2,4,8,或8,4,2 | D.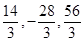 |
设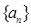 是各项为正数的无穷数列,
是各项为正数的无穷数列,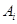 是边长为
是边长为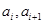 的矩形面积(
的矩形面积(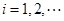 ),则
),则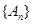 为等比数列的充要条件为
为等比数列的充要条件为
A.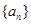 是等比数列。 是等比数列。 |
B.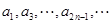 或 或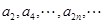 是等比数列。 是等比数列。 |
C.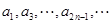 和 和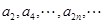 均是等比数列。 均是等比数列。 |
D.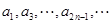 和 和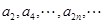 均是等比数列,且公比相同。 均是等比数列,且公比相同。 |
已知等比数列 中,有
中,有 ,数列
,数列 是等差数列,且
是等差数列,且 ,则
,则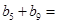 ( )
( )
| A.2 | B.4 | C.8 | D.16 |
已知递增等比数列 满足
满足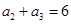 和
和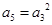 ,则
,则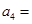
| A.1 | B.8 | C.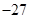 | D.8或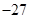 |
设2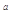 =3,2
=3,2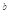 =6,2
=6,2 =12,则数列a,b,c是( )
=12,则数列a,b,c是( )
| A.是等差数列,但不是等比数列 | B.是等比数列,但不是等差数列 |
| C.既是等差数列,又是等比数列 | D.非等差数列,又非等比数列  |
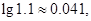
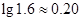 )
)