题目内容
已知点 (
( ,
, )(
)( N*)都在函数
N*)都在函数 (
( )的图象上,则
)的图象上,则 与
与 的大小关系是( )
的大小关系是( )
A. > > | B. < < |
C. = = | D. 与 与 的大小与 的大小与 有关 有关 |
A
解析试题分析:因为点 (
( ,
, )(
)( N*)在函数
N*)在函数 (
( )的图象上,所以
)的图象上,所以 ,所以数列
,所以数列 是等比数列,又a>0且a≠1,所以数列中的每一项都是正的,且两两不等,所以
是等比数列,又a>0且a≠1,所以数列中的每一项都是正的,且两两不等,所以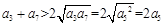 。
。
考点:等比数列的性质。
点评:本题把等比数列的性质和基本不等式相结合,要求学生灵活、熟练掌握每一个知识点。属于基础题型。

练习册系列答案
相关题目
等比数列 中,已知
中,已知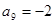 ,则此数列前17项之积为( )
,则此数列前17项之积为( )
A.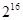 | B. | C. | D. |
已知等比数列{an}公比为q,其前n项和为Sn,若S3,S9,S6成等差数列,则q3等于
A.- | B.1 | C.- 或1 或1 | D.-1或 |
等比数列{an}中,a7=10,q=-2,则a10 =( )
| A.4 | B.40 | C.80 | D.-80 |
设数列{an}.
A.若 =4n,n∈N*,则{an}为等比数列 =4n,n∈N*,则{an}为等比数列 |
B.若an an+2= an+2=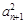 ,n∈N*,则{an}为等比数列 ,n∈N*,则{an}为等比数列 |
C.若am an=2m+n,m,n∈N*,则{an}为等比数列 an=2m+n,m,n∈N*,则{an}为等比数列 |
D.若an an+3=an+1 an+3=an+1 an+2,n∈N*,则{an}为等比数列 an+2,n∈N*,则{an}为等比数列 |
已知数列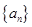 是各项均为正数且公比不等于
是各项均为正数且公比不等于 的等比数列.对于函数
的等比数列.对于函数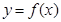 ,若数列
,若数列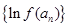 为等差数列,则称函数
为等差数列,则称函数 为“保比差数列函数”.现有定义在
为“保比差数列函数”.现有定义在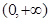 上的如下函数:①
上的如下函数:①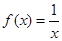 , ②
, ②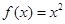 , ③
, ③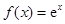 , ④
, ④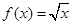 ,
,
则为“保比差数列函数”的所有序号为( )
| A.①② | B.③④ | C.①②④ | D.②③④ |
三个数成等比数列,其和为14,各数平方和为84,则这三个数为( )
| A.2,4,8 | B.8,4,2 |
| C.2,4,8,或8,4,2 | D.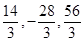 |
已知等比数列 中,有
中,有 ,数列
,数列 是等差数列,且
是等差数列,且 ,则
,则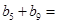 ( )
( )
| A.2 | B.4 | C.8 | D.16 |
若x,2x+2,3x+3是一个等比数列的连续三项,则x的值为 ( )
| A.-4 | B.-1 | C.1或4 | D.-1或-4 |