题目内容
已知函数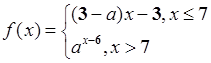 ,若数列
,若数列 满足
满足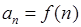 (
(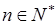 ),且
),且 是递增数列,则实数
是递增数列,则实数 的取值范围是( )
的取值范围是( )
A.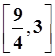 | B.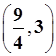 | C.(2,3) | D.(1,3) |
C
解析试题分析:根据题意,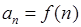 =
=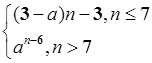 ,要使
,要使 是递增数列,必有
是递增数列,必有 ,解可得2<a<3,故选C.
,解可得2<a<3,故选C.
考点:本题考查了分段函数的性质
点评:考查数列与函数的关系,{an}是递增数列,必须结合f(x)的单调性进行解题,但要注意{an}是递增数列与f(x)是增函数的区别与联系

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
一个等比数列 的前n项和为48,前2n项和为60,则前3n项和为( )
的前n项和为48,前2n项和为60,则前3n项和为( )
| A.63 | B.108 | C.75 | D.83 |
已知等比数列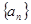 中,各项都是正数,前
中,各项都是正数,前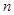 项和为
项和为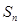 ,且
,且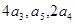 成等差数列,若
成等差数列,若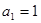 ,则
,则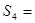 ( )
( )
A.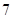 | B.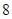 | C.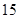 | D.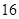 |
在等比数列{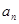 }中,若
}中,若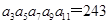 ,则
,则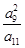 的值为
的值为
| A.9 | B.1 | C.2 | D.3 |
已知数列 是等差数列,
是等差数列,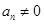 若
若 ,则
,则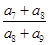 的值是( )
的值是( )
A.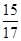 | B.1或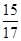 | C.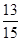 | D.1或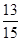 |
设数列{an}.
A.若 =4n,n∈N*,则{an}为等比数列 =4n,n∈N*,则{an}为等比数列 |
B.若an an+2= an+2=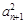 ,n∈N*,则{an}为等比数列 ,n∈N*,则{an}为等比数列 |
C.若am an=2m+n,m,n∈N*,则{an}为等比数列 an=2m+n,m,n∈N*,则{an}为等比数列 |
D.若an an+3=an+1 an+3=an+1 an+2,n∈N*,则{an}为等比数列 an+2,n∈N*,则{an}为等比数列 |
公比为2的等比数列{ } 的各项都是正数,且
} 的各项都是正数,且 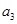
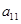 =16,则
=16,则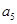 =( )
=( )
| A. 1 | B. 2 | C. 4 | D. 8 |
设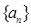 是各项为正数的无穷数列,
是各项为正数的无穷数列,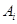 是边长为
是边长为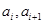 的矩形面积(
的矩形面积(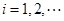 ),则
),则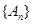 为等比数列的充要条件为
为等比数列的充要条件为
A.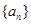 是等比数列。 是等比数列。 |
B.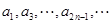 或 或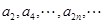 是等比数列。 是等比数列。 |
C.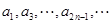 和 和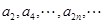 均是等比数列。 均是等比数列。 |
D.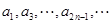 和 和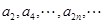 均是等比数列,且公比相同。 均是等比数列,且公比相同。 |
"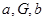 成等比"是"
成等比"是"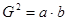 "的 条件( )
"的 条件( )
| A.充要条件 | B.充分不必要 | C.必要不充分 | D.既不充分也不必要 |