题目内容
【题目】已知数列![]() 的前
的前![]() 项和
项和![]() 满足
满足![]() .
.
(1)证明数列![]() 为等差数列,并求出数列
为等差数列,并求出数列![]() 的通项公式.
的通项公式.
(2)若不等式![]() ,对任意
,对任意![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
(3)记数列 的前
的前![]() 项和为
项和为![]() ,是否存在正整数
,是否存在正整数![]() ,
,![]() 使得
使得![]() 成立,若存在,求出所有符合条件的有序实数对(
成立,若存在,求出所有符合条件的有序实数对(![]() ,
,![]() );若不存在,请说明理由.
);若不存在,请说明理由.
【答案】(1)证明见解析,![]() ;(2)
;(2) ![]() ;(3) 存在, (1,1),(1,2).
;(3) 存在, (1,1),(1,2).
【解析】
(1)由![]() 与
与![]() 关系,得出
关系,得出![]() 的递推关系,再用等差数列的定义,证明
的递推关系,再用等差数列的定义,证明![]() 为等差数列,求出其通项,即可求得
为等差数列,求出其通项,即可求得![]() 的通项公式;
的通项公式;
(2)不等式![]() ,对任意
,对任意![]() 恒成立,分离参数转为
恒成立,分离参数转为![]() 对任意
对任意![]() 恒成立,转为求数列
恒成立,转为求数列![]() 的最大值,即可求出结果;
的最大值,即可求出结果;
(3)求出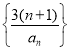 通项公式,以及前
通项公式,以及前![]() 项和为
项和为![]() ,代入
,代入![]() 化简,转化为关于
化简,转化为关于![]() 的不等式,结合
的不等式,结合![]() 为正整数,可求出
为正整数,可求出![]() 的值.
的值.
(1)当![]() =1时,
=1时,![]() ,得
,得![]() ,
,
当![]() 时,
时,![]() ,
,![]() ,
,
两式相减得:![]() ,
,
∴![]() ,即
,即![]() ,
,
又![]() ,
,
∴数列![]() 是以2为首项,1为公差的等差数列.
是以2为首项,1为公差的等差数列.
(2)由(1)知![]() ,即
,即![]()
∵![]()
∴不等式![]() ,对任意
,对任意![]() 恒成立,
恒成立,
等价于![]() 对任意
对任意![]() 恒成立,
恒成立,
记![]()
法一:则![]() 时,
时,![]()
∴![]() 时,
时,![]() ;
;![]() 时,
时,![]() .
.
或(法二):![]() 时,
时,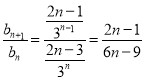
∴当![]() 时,
时,![]() ,
,
∴![]() 或
或![]() 时,
时,![]() 取最大值为
取最大值为![]() ,
,
∴![]() ,即
,即![]()
∴入的取值范围是:![]() .
.
(3)由![]() 得
得![]()
∴数列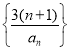 的前
的前![]() 项和为
项和为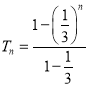 ,
,
则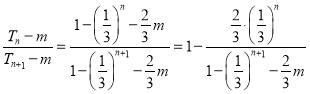
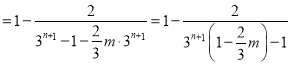
∵![]() ,得
,得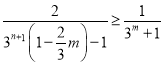
∴![]()
∴![]()
∵![]() 是正整数,∴
是正整数,∴![]()
当![]() 时
时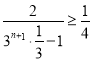 ,即
,即![]()
解得![]() ,
,![]() .
.
综上存在所有符合条件的有序实数对(![]() ,
,![]() )为:(1,1),(1,2).
)为:(1,1),(1,2).

【题目】某地对冬季昼夜温差大小与某反季节大豆新品种发芽多少之间的关系进行分析研究,分别记录了3月1日到3月5日的每天昼夜温差与实验室每天每100颗种子中的发芽数,得到如下资料:
日期 | 3月1日 | 3月2日 | 3月3日 | 3月4日 | 3月5日 |
温差 | 10 | 11 | 13 | 12 | 8 |
发芽数y(颗) | 23 | 25 | 30 | 26 | 16 |
他们所确定的研究方案是:先从这五组数据中选取2组,用剩下的3组数据求线性回归方程,再对选取的2组数据进行检验.
(1)求选取的2组数据恰好是相邻2天数据的概率;
(2)若选取的是3月1日与3月5日的两组数据,请根据3月2日至3月4日的数据,求出y关于x的线性回归方程;并预报当温差为![]() 时的种子发芽数.
时的种子发芽数.
参考公式:![]() ,其中
,其中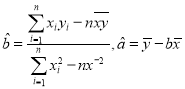
【题目】某校为提高课堂教学效果,最近立项了市级课题《高效课堂教学模式及其运用》,其中王老师是该课题的主研人之一,为获得第一手数据,她分别在甲、乙两个平行班采用“传统教学”和“高效课堂”两种不同的教学模式进行教学实验.为了解教改实效,期中考试后,分别从两个班级中各随机抽取20名学生的成绩进行统计,作出如图所示的茎叶图,成绩大于70分为“成绩优良”.
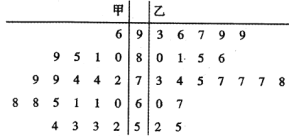
(1)由以上统计数据填写下面![]() 列联表,并判断能否在犯错误的概率不超过
列联表,并判断能否在犯错误的概率不超过![]() 的前提下认为“成绩优良与教学方式有关”?
的前提下认为“成绩优良与教学方式有关”?
甲班 | 乙班 | 总计 | |
成绩优良 | |||
成绩不优良 | |||
总计 |
(2)从甲、乙两班40个样本中,成绩在60分以下(不含60分)的学生中任意选取2人,记来自甲班的人数为![]() ,求
,求![]() 的分布列与数学期望.
的分布列与数学期望.
附: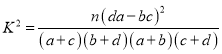 (其中
(其中![]() )
)
|
|
|
|
|
|
|
|
|
|