题目内容
设函数f(x)=sin(2x+ϕ)(-π<ϕ<0),y=f(x)图象的一条对称轴是直线x=
.
(Ⅰ)求ϕ;
(Ⅱ)求函数y=f(x)的单调增区间.
| π |
| 8 |
(Ⅰ)求ϕ;
(Ⅱ)求函数y=f(x)的单调增区间.
(I)函数f(x)=sin(2x+ϕ)图象的对称轴方程为2x+ϕ=
+kπ(k∈Z).
∵直线x=
是函数图象的一条对称轴,∴2•
+ϕ=
+kπ(k∈Z),
结合-π<ϕ<0,取k=-1得ϕ=-
;
(II)由(I)得函数解析式为f(x)=sin(2x-
),
令-
+2mπ≤2x-
≤
+2mπ(m∈Z),得
+mπ≤x≤
+mπ(m∈Z),
∴函数y=f(x)的单调增区间是[
+mπ,
+mπ],(m∈Z).
| π |
| 2 |
∵直线x=
| π |
| 8 |
| π |
| 8 |
| π |
| 2 |
结合-π<ϕ<0,取k=-1得ϕ=-
| 3π |
| 4 |
(II)由(I)得函数解析式为f(x)=sin(2x-
| 3π |
| 4 |
令-
| π |
| 2 |
| 3π |
| 4 |
| π |
| 2 |
| π |
| 8 |
| 5π |
| 8 |
∴函数y=f(x)的单调增区间是[
| π |
| 8 |
| 5π |
| 8 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
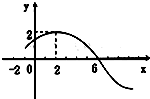

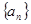 满足:
满足: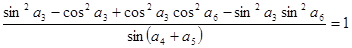 ,公差
,公差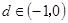 .若当且仅当
.若当且仅当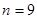 时,数列
时,数列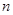 项和
项和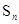 取得最大值,则首项
取得最大值,则首项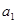 的取值范围是( ).
的取值范围是( ).



 ( )
( )


