题目内容

先将函数y=f（x）的图象向右移
π
6
个单位，再将所得的图象作关于直线x=
π
4
的对称变换，得到y=sin(-2x+
π
3
)的函数图象，则f（x）的解析式是（　　）
A．y=sin(-2x+
π
3
)		B．y=sin(-2x-
π
3
)
C．y=sin(2x-
π
3
)		D．y=sin(2x+
π
3
)
设函数为y=g（x）的图象与函数y=sin（-2x+
π
3
）的图象关于直线x=
π
4
对称，
则g（x）=sin[-2（
π
2
-x）+
π
3
]=sin（2x-
2π
3
），
∴f（x）=g（x+
π
6
）=sin[2（x+
π
6
）-
2π
3
]=sin（2x-
π
3
），
故选：C．
练习册系列答案
相关题目
把函数y=2+cos2x的图象上所有点的横坐标伸长到原来的2倍（纵坐标不变），然后向左平移1个单位长度，再向下平移2个单位长度，得到的函数的解析式是（　　）
A．y=cos（x+1）B．y=cos（x-1）C．y=cos（4x+4）D．y=cos（4x+1）
已知函数f（x）=Asin（ωx+ϕ）的导函数f′（x）在一个周期内的图象如右图，则下列函数f（x）的解析式中，满足条件的是（　　）
A．y=sin(2x+
π
6
)		B．y=sin(2x+
π
3
)
C．y=2sin(2x+
π
6
)		D．y=2sin(2x+
π
3
)
设函数f（x）=sin（2x+ϕ）（-π＜ϕ＜0），y=f（x）图象的一条对称轴是直线x=
π
8
．
（Ⅰ）求ϕ；
（Ⅱ）求函数y=f（x）的单调增区间．
函数f（x）=3sin（2x-
π
3
）-2图象的一条对称轴是（　　）
A．x=
π
6
B．x=
π
3
C．x=
5π
12
D．x=
7π
12
函数f(x)=Asin(ωx+φ)，x∈R(A＞0，ω＞0，|φ|＜
π
2
)的一段图象如图5所示：将y=f（x）的图象向右平移m（m＞0）个单位，可得到函数y=g（x）的图象，且图象关于原点对称，g(
π
2013
)＞0．
（1）求A、ω、φ的值；
（2）求m的最小值，并写出g（x）的表达式；
（3）若关于x的函数y=g(
tx
2
)在区间[-
π
3
，
π
4
]上最小值为-2，求实数t的取值范围．
函数f（x）=Asinωx（A＞0，ω＞0）的部分图象如图所示，则f（1）+f（2）+f（3）+…+f（2010）的值为（　　）
A．2B．
2
C．2-
2
D．2+
2
要得到函数y=3sin（2x+
π
3
）的图象，只要把函数y=3sin2x图象（　　）
A．向右平移
π
3
个单位		B．向左平移
π
3
个单位
C．向右平移
π
6
个单位		D．向左平移
π
6
个单位
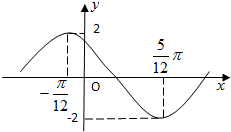
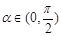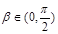设，，且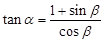，则下列关系成立的是（   ）.
A．B．C．D．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网