题目内容
已知向量
=(sinx,2
sinx),
=(2cosx,sinx),设f(x)=
•
-
(1)求函数y=f(x)的单调递减区间;
(2)若0<θ<
,且y=f(x+θ)为偶函数,求θ的值.
| a |
| 3 |
| b |
| a |
| b |
| 3 |
(1)求函数y=f(x)的单调递减区间;
(2)若0<θ<
| π |
| 2 |
(1)∵f(x)=
•
-
=2sinxcosx+2
sin2x=sin2x+2
×
=sin2x-
cos2x+
=2sin(2x-
)+
,
令 2kπ+
≤2x-
≤2kπ+
,k∈z,
可得 kπ+
≤2x-
≤2kπ+
,k∈z,
故函数的减区间为[kπ+
,2kπ+
],k∈z.
(2)若0<θ<
,且y=f(x+θ)=2sin[2(x+θ)-
]+
=2sin(2x+2θ-
)为偶函数,
则有 2θ-
=
,
θ=
.
| a |
| b |
| 3 |
| 3 |
| 3 |
| 1-cos2x |
| 2 |
=sin2x-
| 3 |
| 3 |
| π |
| 3 |
| 3 |
令 2kπ+
| π |
| 2 |
| π |
| 3 |
| 3π |
| 2 |
可得 kπ+
| 5π |
| 12 |
| π |
| 3 |
| 11π |
| 12 |
故函数的减区间为[kπ+
| 5π |
| 12 |
| 11π |
| 12 |
(2)若0<θ<
| π |
| 2 |
| π |
| 3 |
| 3 |
| π |
| 3 |
则有 2θ-
| π |
| 3 |
| π |
| 2 |
θ=
| 5π |
| 12 |

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目



 ,
, 则
则 .
.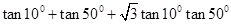 的值为( )
的值为( )


