题目内容
【题目】已知实数x，y满足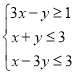
，则
的最大值为________，
的最小值为________.
【答案】6 
【解析】
在平面直角坐标系内画出不等式组的表示的平面区域.
空一：平行移动直线
，在平面区域内，找到一点使得直线
在纵轴上的截距最大，求出点的坐标代入目标函数中即可；
空二：对目标函数进行变形为斜率模型，利用斜率的几何意义进行求解即可.
在平面直角坐标系内画出不等式组的表示的平面区域如下图所示.
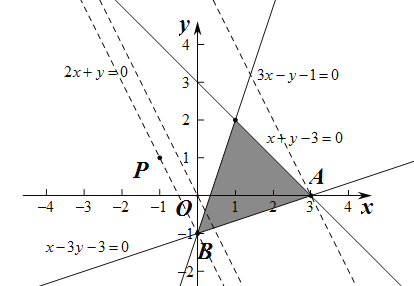
空一：在平面区域内，平行移动直线，当直线经过点
时，该直线在纵轴上的截距最大，点的坐标就是直线
与横轴交点的坐标，即
，
所以
的最大值为：
；
空二：
，其中
，要想求
的最小值，就是求
的最小值，的几何意义就是平面区域内一点与点
的斜率，显然平面区域由点
与点的斜率最小，最小值为：
，
所以
.
故答案为：6；
【题目】总体由编号为
的20个个体组成,利用下面的随机数表选取6个个体,选取方法是从随机数表第一行的第5列和第6列数字开始由左到右依次选取两个数字,则选出来的第6个个体的编号为( )
7816 | 6572 | 0802 | 6314 | 0702 | 4369 | 1128 | 0598 |
3204 | 9234 | 4935 | 8200 | 3623 | 4869 | 6938 | 7481 |
A.08B.07C.02D.05
【题目】2017年某市有2万多文科考生参加高考，除去成绩为
分（含分）以上的3人与成绩为
分（不含分）以下的3836人，还有约1.9万文科考生的成绩集中在
内，其成绩的频率分布如下表所示：
分数段 |
|
|
|
|
频率 | 0.108 | 0.133 | 0.161 | 0.183 |
分数段 |
|
|
|
|
频率 | 0.193 | 0.154 | 0.061 | 0.007 |
（Ⅰ）试估计该次高考成绩在内文科考生的平均分（精确到
）；
（Ⅱ）一考生填报志愿后，得知另外有4名同分数考生也填报了该志愿.若该志愿计划录取3人，并在同分数考生中随机录取，求该考生不被该志愿录取的概率.