题目内容
5.以原点O和A(4,2)为两个顶点作等腰三角形OAB,∠OBA=90°,则点B的坐标为( )| A. | (1,3)或(3,-1) | B. | (-1,3)或(3,1) | C. | (1,3)或(3,1) | D. | (1,3) |
分析 设B(x,y),利用三角形是等腰直角三角形得到向量$\overrightarrow{OB}$⊥$\overrightarrow{AB}$,C为OA中点得到$\overrightarrow{OC}$⊥$\overrightarrow{BC}$,由此得到关于B的坐标的方程解之.
解答 解:设点B的坐标为(x,y),则$\overrightarrow{OB}$=(x,y),$\overrightarrow{AB}$=(x-4,y-2).
∵∠OBA=90°,即$\overrightarrow{OB}$⊥$\overrightarrow{AB}$,∴$\overrightarrow{OB}•\overrightarrow{AB}$=0,
∴x(x-4)+y(y-2)=0,
即x2+y2-4x-2y=0,①
设OA的中点为C,则点C(2,1),$\overrightarrow{OC}$=(2,1),$\overrightarrow{BC}$=(x-2,y-1),
在等腰三角形AOB中,$\overrightarrow{OC}$⊥$\overrightarrow{BC}$,所以$\overrightarrow{OC}•\overrightarrow{BC}$=0,
∴2(x-2)+y-1=0,即2x+y-5=0,②
解①②得$\left\{\begin{array}{l}{x=1}\\{y=3}\end{array}\right.$或$\left\{\begin{array}{l}{x=3}\\{y=-1}\end{array}\right.$
故B点坐标为(1,3)或(3,-1);
故选A.
点评 本题考查了利用平面向量的坐标运算、向量垂直求点的坐标;关键是由已知适当设点,利用等腰直角三角形的性质得到向量垂直.

| A. | 函数的最小正周期为$\frac{π}{2}$ | B. | 函数关于($\frac{π}{6}$,0)中心对称 | ||
| C. | 函数在-$\frac{π}{12}$处取得最大值 | D. | 函数在(-$\frac{π}{12}$,$\frac{π}{6}$)单调递减 |
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
| x | 10 | 15 | 20 | 25 | 30 |
| y | 1 003 | 1 005 | 1 010 | 1 011 | 1 014 |
| A. | $\stackrel{∧}{y}$=0.63x-231.2 | B. | $\stackrel{∧}{y}$=0.56x+997.4 | C. | $\stackrel{∧}{y}$=50.2x+501.4 | D. | $\stackrel{∧}{y}$=60.4x+400.7 |
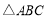 中,
中,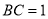 ,
,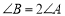 ,
,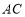 的取值范围为( )
的取值范围为( )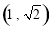 B.
B.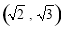
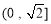 D.
D.