题目内容
15.已知向量$\overrightarrow{m}$=(sin$\frac{x}{3}$,-1),$\overrightarrow{n}$=($\frac{\sqrt{3}}{2}$A,$\frac{1}{2}$Acos$\frac{x}{3}$)(A>0),函数f(x)=$\overrightarrow{n}$•$\overrightarrow{m}$的最大值为2.(1)求f(x)最小正周期和解析式;
(2)设α,β∈[0,$\frac{π}{2}$],f(3α+$\frac{π}{2}$),f(3β+2π)=$\frac{6}{5}$,求sin(α-β)的值.
分析 (1)利用平面向量的数量积得到解析式,然后利用三角函数公式化简,由题意得到周期和A;
(2)由(1)得到α,β的三角函数值,然后由两角和与差的三角函数公式求值.
解答 解:(1)$f(x)=\frac{{\sqrt{3}}}{2}Asin\frac{x}{3}-\frac{1}{2}Acos\frac{x}{3}=A({\frac{{\sqrt{3}}}{2}sin\frac{x}{3}-\frac{1}{2}cos\frac{x}{3}})=Asin({(\frac{x}{3}-\frac{π}{6}})$…(3分)
f(x)的最小正周期$T=\frac{2π}{{\frac{1}{3}}}=6π$…(4分)
因为 A>0,由题意知A=2,…(5分)
所以f(x)=2sin($\frac{1}{3}$x-$\frac{π}{6}$)…(6分)
(2)f(3α+$\frac{π}{2}$)=2sin($\frac{1}{3}$(3α+$\frac{π}{2}$)-$\frac{π}{6}$)=2sinα=$\frac{10}{13}$,
f(3β+2π)=2sin($\frac{1}{3}$(3β+2π)-$\frac{π}{6}$)=2sin($β+\frac{π}{2}$)=2cosβ=$\frac{6}{5}$,…(8分)
∴sin$α=\frac{5}{13}$,cos$β=\frac{3}{5}$,α,β∈[0,$\frac{π}{2}$],
∴cosα=$\sqrt{1-si{n}^{2}α}$=$\frac{12}{13}$
sinβ=$\sqrt{1-co{s}^{2}β}$=$\frac{4}{5}$ …(10分)
∴sin(α-β)=sinαcosβ-cosαsinβ=$\frac{5}{13}×\frac{3}{5}-\frac{12}{13}×\frac{4}{5}$=-$\frac{33}{65}$ …(12分)
点评 本题考查了平面向量的数量积、三角函数式的化简以及三角函数公式;熟练掌握两角和与差的三角函数公式是关键.

| A. | (1,3)或(3,-1) | B. | (-1,3)或(3,1) | C. | (1,3)或(3,1) | D. | (1,3) |
| A. | [2,+∞) | B. | (2,+∞) | C. | (-∞,2] | D. | (-∞,2) |
| A. | (4,+∞) | B. | [6,8) | C. | (6,8) | D. | (1,8) |
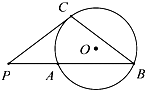 如图,PC是⊙O的切线,C为切点,PAB为割线,PC=2,PA=1,∠P=60°,则BC=( )
如图,PC是⊙O的切线,C为切点,PAB为割线,PC=2,PA=1,∠P=60°,则BC=( )| A. | 3 | B. | 2 | C. | 3$\sqrt{2}$ | D. | 2$\sqrt{3}$ |