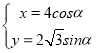题目内容
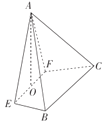
【题目】如图, 在四棱锥![]() 中,
中,![]() 为等边三角形, 平面
为等边三角形, 平面![]() 平面
平面![]() ,四边形
,四边形![]() 是高为
是高为![]() 的等腰梯形,
的等腰梯形,![]() 为
为![]() 的中点.
的中点.
(1)求证:![]() ;
;
(2)求![]() 到平面
到平面![]() 的距离.
的距离.
【答案】(1)详见解析(2)![]()
【解析】
试题分析:(1)证明线线垂直,一般利用线面垂直判定与性质定理,经多次转化得证,而其中转化时,往往需结合平几中垂直条件,如等比三角形中线垂直底边,对应面面垂直条件,一般利用面面垂直性质定理将其转化为线面垂直,即由平面![]() 平面
平面![]() 平面
平面![]() 得
得![]() 平面
平面![]() ,(2)求点到面距离,一般利用等体积法求高或根据线面垂直作高,由于(1)知
,(2)求点到面距离,一般利用等体积法求高或根据线面垂直作高,由于(1)知![]() 平面
平面![]() ,因而可将其转化为面面垂直:取
,因而可将其转化为面面垂直:取![]() 的中点
的中点![]() ,则平面
,则平面![]() 平面
平面![]() ,再过
,再过![]() 作
作![]() ,则得
,则得![]() 平面
平面![]() ,即
,即![]() 到平面
到平面![]() 的距离,然后在对应三角形中求解即可.
的距离,然后在对应三角形中求解即可.
试题解析:(1)证明:因为![]() 是等边三角形,
是等边三角形,![]() 为
为![]() 的中点, 所以
的中点, 所以![]() .又因为平面
.又因为平面![]() 平面
平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,所以
,所以![]() .
.
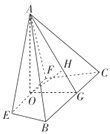
(2)取![]() 的中点
的中点![]() ,连接
,连接![]() ,由题设知,
,由题设知,![]() , 由(1) 知
, 由(1) 知![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,所以
,所以![]() .因为
.因为![]() ,所以
,所以![]() 平面
平面![]() .过
.过![]() 作
作![]() ,垂足为
,垂足为![]() ,则
,则![]() ,因为
,因为![]() ,所以
,所以![]() 平面
平面![]() .因为
.因为![]() ,所以
,所以![]() ,即
,即![]() 到平面
到平面![]() 的距离为
的距离为![]() .(另外用等体积法亦可)
.(另外用等体积法亦可)

练习册系列答案
相关题目
【题目】汕尾市基础教育处为调查在校中学生每天放学后的自学时间情况,在本市的所有中学生中随机抽取了120名学生进行调查,现将日均自学时间小于1小时的学生称为“自学不足”者![]() 根据调查结果统计后,得到如下
根据调查结果统计后,得到如下![]() 列联表,已知在调查对象中随机抽取1人,为“自学不足”的概率为
列联表,已知在调查对象中随机抽取1人,为“自学不足”的概率为![]() .
.
非自学不足 | 自学不足 | 合计 | |
配有智能手机 | 30 | ||
没有智能手机 | 10 | ||
合计 |
![]() 请完成上面的列联表;
请完成上面的列联表;
![]() 根据列联表的数据,能否有
根据列联表的数据,能否有![]() 的把握认为“自学不足”与“配有智能手机”有关?
的把握认为“自学不足”与“配有智能手机”有关?
附表及公式: ![]() ,其中
,其中![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|