Question

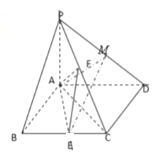
【题目】如图所示，由一块扇形空地，其中，米，计划在此扇形空地区域为学生建灯光篮球运动场，区域内安装一批照明灯，点、选在线段上（点、分别不与点、重合），且.

（1）若点在距离点米处，求点、之间的距离；

（2）为了使运动场地区域最大化，要求面积尽可能的小，记，请用表示的面积，并求的最小值.

Answer 1

【答案】（1）米；（2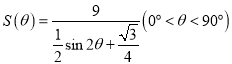），最小面积为平方米.

【解析】

（1）利用余弦定理求得的长度，并求出，可得出，可得出，进而可求得的长度；

（2）利用正弦定理求出、关于的表达式，利用三角形的面积公式可得出的表达式，结合三角恒等变换思想化简，利用正弦型函数的有界性可求得的最小值.

（1）在中，，，

由余弦定理得，，

中，由，解得，

即，故，可知，求得，因此，（米）；

（2）记，则有，，，

由正弦定理可得，，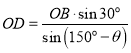

，

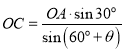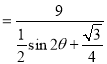由，则，则当时，即当时，有最小值平方米