题目内容
12. 如图,点A、B、C都在⊙O上,过点C的切线交AB的延长线于点D,若AB=6,BC=3,CD=4,则线段AC的长为6.
如图,点A、B、C都在⊙O上,过点C的切线交AB的延长线于点D,若AB=6,BC=3,CD=4,则线段AC的长为6.
分析 根据圆的切线和割线,利用切割线定理得到与圆有关的比例线段,代入已知线段的长度求出DB的长,根据三角形的两个角对应相等,得到两个三角形全等,对应线段成比例,得到要求的线段的长度.
解答 解: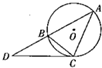 ∵过点C的切线交AB的延长线于点D,
∵过点C的切线交AB的延长线于点D,
∴DC是圆的切线,DBA是圆的割线,
根据切割线定理得到DC2=DB•DA,
∵AB=6,CD=4,
∴16=DB(DB+6)
∴DB=2,
由题意知∠D=∠D,∠BCD=∠A
∴△DBC∽△DCA,
∴$\frac{DC}{DA}=\frac{BC}{CA}$
∴AC=$\frac{8×3}{4}$=6,
故答案为:6.
点评 本题考查与圆有关的比例线段,考查三角形的相似的判定定理与性质定理,本题解题的关键是根据圆中的比例式,代入已知线段的长度求出未知的线段的长度,本题是一个基础题.

练习册系列答案
相关题目
3.己知等差数列{an}的首项为a1,公差为d,其前n项和为Sn,若直线y=a1x与圆(x-1)2+y2=1的两个交点关于直线x+y+d=0对称,则Sn=( )
| A. | n2 | B. | -n2 | C. | $\frac{-{n}^{2}+3n}{2}$ | D. | n2-2n |
20.观察下列各式:55=3125,56=15625,57=78125,…,则52015的末四位数字为( )
| A. | 3125 | B. | 5625 | C. | 0625 | D. | 8125 |