题目内容
已知矩阵A=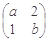 有一个属于特征值1的特征向量
有一个属于特征值1的特征向量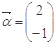 .
.
(Ⅰ) 求矩阵A;
(Ⅱ) 若矩阵B=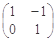 ,求直线
,求直线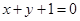 先在矩阵A,再在矩阵B的对应变换作用下的像的方程.
先在矩阵A,再在矩阵B的对应变换作用下的像的方程.
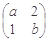 有一个属于特征值1的特征向量
有一个属于特征值1的特征向量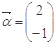 .
.(Ⅰ) 求矩阵A;
(Ⅱ) 若矩阵B=
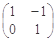 ,求直线
,求直线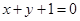 先在矩阵A,再在矩阵B的对应变换作用下的像的方程.
先在矩阵A,再在矩阵B的对应变换作用下的像的方程. (1)A= .(2)
.(2)
 .(2)
.(2)
试题分析:(Ⅰ)由已知得
 ,所以
,所以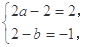 2分
2分解得
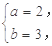 故A=
故A= . ……………………………………………………3分
. ……………………………………………………3分(Ⅱ) BA=
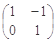
 =
= ,因为矩阵BA所对应的线性变换将直线变成直线(或点),所以可取直线
,因为矩阵BA所对应的线性变换将直线变成直线(或点),所以可取直线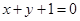 上的两点(0,1),(-1,2), 4分
上的两点(0,1),(-1,2), 4分 ,
, ,由得:(0,1),(-1,2)在矩阵A所对应的线性变换下的像是点(1,-3),(-1,-1) 6分
,由得:(0,1),(-1,2)在矩阵A所对应的线性变换下的像是点(1,-3),(-1,-1) 6分从而直线
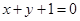 在矩阵BA所对应的线性变换下的像的方程为
在矩阵BA所对应的线性变换下的像的方程为 . 7分
. 7分点评:主要是考查了矩阵的计算以及变换的运用,属于基础题。

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
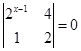 ,则
,则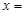 .
.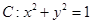 在矩阵
在矩阵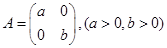 对应的变换下变成椭圆
对应的变换下变成椭圆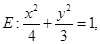 求矩阵
求矩阵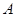 的逆矩阵
的逆矩阵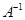 .
.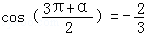 ,则cos2α= .
,则cos2α= .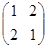 的特征值
的特征值 所对应的一个特征向量。
所对应的一个特征向量。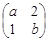 有一个属于特征值1的特征向量
有一个属于特征值1的特征向量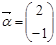 .
.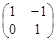 ,点O(0,0),M(2,-1),N(0,2),求
,点O(0,0),M(2,-1),N(0,2),求 在矩阵AB的对应变换作用下所得到的
在矩阵AB的对应变换作用下所得到的 的面积.
的面积. 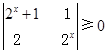 的解为 .
的解为 . ,B=
,B= ,C=
,C= ,求AB和AC.
,求AB和AC.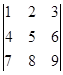 中元素8的代数余子式为______________.
中元素8的代数余子式为______________.