题目内容
(本小题满分8分)如图,矩形ABCD中,AD^平面ABE,AE=EB=BC=2,F为CE上的一点,且BF^平面ACE,AC与BD交于点G。

(1)求证:AE^平面BCE;
(2)求证:AE//平面BFD;
(3)求三棱锥C-BFG的体积。

(1)求证:AE^平面BCE;
(2)求证:AE//平面BFD;
(3)求三棱锥C-BFG的体积。
(1)证明:因为AD^平面ABE,AD//BC
所以BC^平面ABE
因为AE^BC,又因为BF^平面ACE
∴AE^BF,因为BC∩BF=B
且BC,BFÌ平面BCE
所以AE^平面BCE…………………………3分
(2)证明:依题意可知点G是AC的中点。
由BF^平面ACE,知CE^BF
而BC=BE,所以点F是EC中点。
所以在DAEC中,FG//AE
又因为FGÌ平面BFD,AEË平面BFD
所以,AE//平面BFD…………………………5分
(3)解:因为AE//FG且AE^平面BCE
所以FG//平面BCE,即FG^平面BCF
因为点G是AC中点,F是CE中点,
所以FG=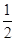 AE=1
AE=1
又知RtDBCE中,CE=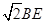 =
=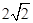
BF=CF=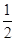 CE=
CE=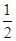
所以SDBCF=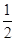 ´
´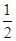 ´
´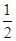 =1
=1
所以VC-BFG=VG-BCF=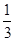 ´SDBCF´FG=
´SDBCF´FG=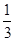 ………………8分
………………8分
所以BC^平面ABE
因为AE^BC,又因为BF^平面ACE
∴AE^BF,因为BC∩BF=B
且BC,BFÌ平面BCE
所以AE^平面BCE…………………………3分
(2)证明:依题意可知点G是AC的中点。
由BF^平面ACE,知CE^BF
而BC=BE,所以点F是EC中点。
所以在DAEC中,FG//AE
又因为FGÌ平面BFD,AEË平面BFD
所以,AE//平面BFD…………………………5分
(3)解:因为AE//FG且AE^平面BCE
所以FG//平面BCE,即FG^平面BCF
因为点G是AC中点,F是CE中点,
所以FG=
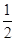 AE=1
AE=1又知RtDBCE中,CE=
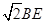 =
=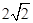
BF=CF=
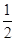 CE=
CE=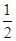
所以SDBCF=
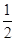 ´
´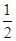 ´
´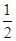 =1
=1所以VC-BFG=VG-BCF=
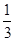 ´SDBCF´FG=
´SDBCF´FG=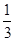 ………………8分
………………8分略

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 的边长为2,点
的边长为2,点 、
、 分别在边
分别在边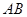 、
、 上,且
上,且 ,
, ,将此正方形沿
,将此正方形沿 、
、 折起,使点
折起,使点 、
、 重合于点
重合于点 ,则三棱锥
,则三棱锥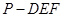 的体积是
的体积是



 ,其余棱长都为1,其体积为
,其余棱长都为1,其体积为 ,则函数
,则函数 中,
中,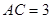 ,
,  ,点
,点 是
是 的中点.
的中点. ;
; 平面
平面 ;
; 的体积.
的体积.






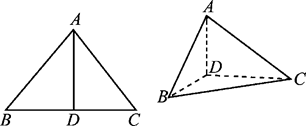
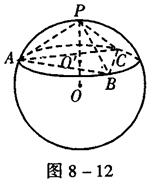
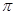 ,球心到该截面的距离为
,球心到该截面的距离为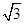 ,则球的表面积是( )
,则球的表面积是( )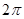



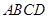 ,则以
,则以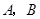 为焦点,且过
为焦点,且过 两点的椭圆的离心率为
两点的椭圆的离心率为