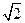题目内容
(12分) 如图8-12,球面上有四个点P、A、B、C,如果PA,PB,PC两两互相垂直,且PA=PB=PC=a,求这个球的表面积。

解 如图8-12,设过A、B、C三点的球的截面圆半径为r,圆心为O′,球心到该圆面的距离为d。在三棱锥P—ABC中,
∵PA,PB,PC两两互相垂直,且PA=PB=PC=a,
∴AB=BC=CA=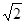 a,且P在△ABC内的射影即是△ABC的中心O′。
a,且P在△ABC内的射影即是△ABC的中心O′。
由正弦定理,得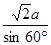 =2r,∴r=
=2r,∴r=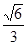 a。
a。
又根据球的截面的性质,有OO′⊥平面ABC,而PO′⊥平面ABC,
∴P、O、O′共线,球的半径R= 。又PO′=
。又PO′=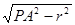 =
=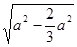 =
=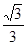 a,
a,
∴OO′="R" -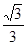 a=d=
a=d= ,(R-
,(R-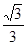 a)2=R2 – (
a)2=R2 – (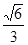 a)2,解得R=
a)2,解得R=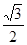 a,
a,
∴S球=4πR2=3πa2。
∵PA,PB,PC两两互相垂直,且PA=PB=PC=a,
∴AB=BC=CA=
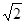 a,且P在△ABC内的射影即是△ABC的中心O′。
a,且P在△ABC内的射影即是△ABC的中心O′。由正弦定理,得
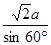 =2r,∴r=
=2r,∴r=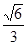 a。
a。又根据球的截面的性质,有OO′⊥平面ABC,而PO′⊥平面ABC,
∴P、O、O′共线,球的半径R=
 。又PO′=
。又PO′=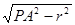 =
=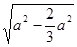 =
=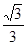 a,
a,∴OO′="R" -
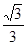 a=d=
a=d= ,(R-
,(R-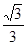 a)2=R2 – (
a)2=R2 – (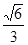 a)2,解得R=
a)2,解得R=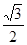 a,
a,∴S球=4πR2=3πa2。
略

练习册系列答案
相关题目
 ,
, ,
, 为棱
为棱 的中点,AC与BD交于点O.(1)求证:
的中点,AC与BD交于点O.(1)求证:
 ;
;  的体积.
的体积.

 中,
中,  、
、 、
、 两两垂直,且
两两垂直,且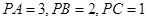 .设
.设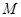 是底面
是底面 内一点,定义
内一点,定义 ,其中
,其中 、
、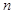 、
、 分别是三棱锥
分别是三棱锥 、 三棱锥
、 三棱锥 、三棱锥
、三棱锥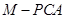 的体积.已知
的体积.已知 .
. 的值;
的值; 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.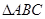 中,
中, ,
, ,
, ,如图所示。若将
,如图所示。若将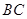 旋转一周,则所形成的旋转体的体积是( )
旋转一周,则所形成的旋转体的体积是( ) 



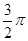
 在直观图中,
在直观图中, 是
是 的中点,
的中点, 是
是 的中点,侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
的中点,侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.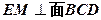 ;
; 的体积。
的体积。


 是边长为1的正方形,则该几何体的体积为( )
是边长为1的正方形,则该几何体的体积为( )