Question

【题目】已知圆O：x2+y2=16及圆内一点F（﹣3，0），过F任作一条弦AB．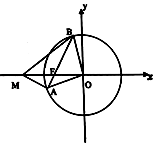
（1）求△AOB面积的最大值及取得最大值时直线AB的方程；
（2）若点M在x轴上，且使得MF为△AMB的一条内角平方线，求点M的坐标．

Answer 1

【答案】
（1）解：设∠AOB=θ，则 ，

当 时，S△AOBmax=8，此时O到AB的距离为 ， ，

∴S△AOBmax=8，直线AB的方程为

（2）解：当直线AB斜率不存在时，MF始终平分∠AMB．

当直线AB斜率存在时，设直线AB：y=k（x+3），（k≠0），设M（m，0），

由 得：（1+k2）x2+6k2x+（9k2﹣16）=0

设A（x1，y1），B（x2，y2），则 ， ．

∵∠BMF=∠AMF，

∴kBM+kAM=0， ，

∴（x1+3）（x2﹣m）+（x2+3）（x1﹣m）=0，

∴2x1x2+（3﹣m）（x1+x2）﹣6m=0，

∴ ，

∴﹣32﹣6m=0， ，

∴

【解析】（1）设∠AOB=θ，则 ，即可求△AOB面积的最大值及取得最大值时直线AB的方程；（2）分类讨论，由 得：（1+k2）x2+6k2x+（9k2﹣16）=0，利用∠BMF=∠AMF，kBM+kAM=0，即可得出结论．