题目内容
【题目】已知数列{an}的前项n和为Sn , 且3Sn=4an﹣4.又数列{bn}满足bn=log2a1+log2a2+…+log2an .
(1)求数列{an}、{bn}的通项公式;
(2)若 ![]() ,求使得不等式
,求使得不等式 ![]() 恒成立的实数k的取值范围.
恒成立的实数k的取值范围.
【答案】
(1)解:由3Sn=4an﹣4可得a1=4,
∵3Sn=4an﹣4,∴3Sn﹣1=4an﹣1﹣4,∴3Sn﹣3Sn﹣1=4an﹣4﹣(4an﹣1﹣4),
∴3an=4an﹣4an﹣1,即 ![]() .
.
∴数列{an}是首项为a1=4,公比为4的等比数列,∴ ![]() .
.
又bn=log2a1+log2a2+…+log2an=2+4+…+2(n﹣1)+2n=n(n+1),
∴bn=n(n+1)
(2)解: ![]() =1﹣
=1﹣ ![]() +
+ ![]() ﹣
﹣ ![]() +…+
+…+ ![]() ﹣
﹣ ![]() =
= ![]() ,
,
不等式 ![]() 恒成立,即k≥
恒成立,即k≥ ![]() 恒成立,
恒成立,
设dn= ![]() ,则dn+1﹣dn=
,则dn+1﹣dn= ![]() ,
,
∴当n≥2时,数列{dn}单调递减,当1≤n<2时,数列{dn}单调递增;
即d1<d2>d3>d4>…,
∴数列最大项为 ![]() ,∴
,∴ ![]()
【解析】(1)利用再写一式,两式相减的方法求数列{an}的通项公式、利用数列{bn}满足bn=log2a1+log2a2+…+log2an , 求出{bn}的通项公式;(2)若 ![]() ,裂项求和,不等式
,裂项求和,不等式 ![]() 恒成立,即k≥
恒成立,即k≥ ![]() 恒成立,即可实数k的取值范围.
恒成立,即可实数k的取值范围.
【考点精析】本题主要考查了数列的前n项和的相关知识点,需要掌握数列{an}的前n项和sn与通项an的关系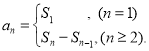 才能正确解答此题.
才能正确解答此题.

练习册系列答案
相关题目