Question

【题目】如图，在直四棱柱ABCD﹣A1B1C1D1中，底面ABCD是边长2的正方形，E，F分别为线段DD1 ， BD的中点．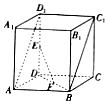
（1）求证：EF∥平面ABC1D1；
（2）AA1=2 ，求异面直线EF与BC所成的角的大小．

Answer 1

【答案】
（1）证明：连结BD1，

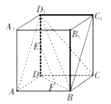
在△DD1B中，E、F分别是D1D、DB的中点，

∴EF是△DD1B的中位线，

∴EF∥D1B，

∵D1B平面ABC1D1，EF平面ABC1D1，

∴EF∥平面ABC1D1

（2）解：∵AA1=2 ，AB=2，EF∥BD1，

∴∠D1BC是异面直线EF与BC所成的角（或所成角的补角），

在直四棱柱ABCD﹣A1B1C1D1中，BC⊥平面CDD1C1，CD1平面CDD1C1，

∴BC⊥CD1．

在Rt△D1C1C中，BC=2，CD1=2 ，D1C⊥BC，

∴tan∠D1BC= ，

∴∠D1BC=60°，

∴异面直线EF与BC所成的角的大小为60°

【解析】（1）连结BD1 ， 推导出EF∥D1B，由此能证明EF∥平面ABC1D1 ． （2）由EF∥BD1 ， 知∠D1BC是异面直线EF与BC所成的角（或所成角的补角），由此能求出异面直线EF与BC所成的角的大小．
【考点精析】认真审题，首先需要了解异面直线及其所成的角(异面直线所成角的求法：1、平移法：在异面直线中的一条直线中选择一特殊点，作另一条的平行线；2、补形法：把空间图形补成熟悉的或完整的几何体，如正方体、平行六面体、长方体等，其目的在于容易发现两条异面直线间的关系)，还要掌握直线与平面平行的判定(平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行；简记为：线线平行，则线面平行)的相关知识才是答题的关键．