��Ŀ����
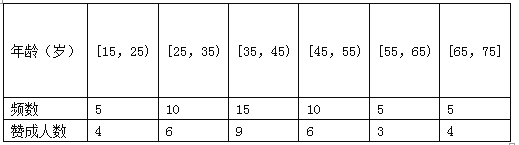
����Ŀ��ijʡ�߿��ĸ�ʵʩ����ָ������ʡ�߿������ܳɼ��������ġ���ѧ������3��ͳһ�߿��ɼ���ѧ������ѡ���ѧҵˮƽ�ȼ��Կ��Կ�Ŀ��ͬ���ɣ���ʡ������Ϊ�˽����ڶ����е�ѧ���ҳ��Ը߿��ĸ﷽�����ֵ���̬�ȣ�������г�ȡ��100������ҳ���Ϊ�������е��飬��������ʾ��������25�˳ֲ����������ͼ�Ǹ��������ĵ��������Ƶĵȸ�����ͼ.
��1��������֪������ȸ�����ͼ��������![]() �����������ж������ܷ���95%�İ�����Ϊ���ɸ߿��ĸ﷽������继���йء���
�����������ж������ܷ���95%�İ�����Ϊ���ɸ߿��ĸ﷽������继���йء���

ע��![]() ������
������![]() .
.

��2����������Ƶ�ʹ��Ƹ��ʣ��������ȫʡ���ɸ߿��ĸ�ļҳ��г�ȡ3��������3���ҳ����dz��ڵ�����Ϊ![]() ������
������![]() �ķֲ��м���ѧ����
�ķֲ��м���ѧ����![]() .
.
���𰸡�(1)�𰸼�������(2)�𰸼�����.
�������������������1���ɵȸ�����ͼ�����![]() ���������ɿ�����ʽ���
���������ɿ�����ʽ���![]() ���ɵ�����û��95%�İ�����Ϊ���ɸ߿��ĸ﷽������继���йء�����2��
���ɵ�����û��95%�İ�����Ϊ���ɸ߿��ĸ﷽������继���йء�����2��
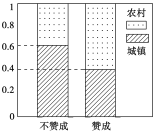
��������Ƶ�ʹ��Ƹ��ʣ������ȫʡ���ɸ߿��ĸ�ļҳ��г��г��ڼҳ��ĸ���Ϊ0.6.����ũ�廧�ڼҳ��ĸ���Ϊ0.4�������������ֲ����ɶ���ֲ���ʽд��![]() �ķֲ��м���ѧ������
�ķֲ��м���ѧ������
�����������1�����![]() �����������£�
�����������£�

���빫ʽ����![]() �۲�ֵ��
�۲�ֵ��
![]()
![]() .
.
������û��95%�İ�����Ϊ���ɸ߿��ĸ﷽������继���йء�.
��2����������Ƶ�ʹ��Ƹ��ʣ������ȫʡ���ɸ߿��ĸ�ļҳ��г��г��ڼҳ��ĸ���Ϊ0.6.
����ũ�廧�ڼҳ��ĸ���Ϊ0.4��
![]() �Ŀ���ȡֵΪ0��1��2��3.
�Ŀ���ȡֵΪ0��1��2��3.
![]() ��
��
![]() ��
��
![]() ��
��
![]() .
.
��![]() �ķֲ���Ϊ��
�ķֲ���Ϊ��
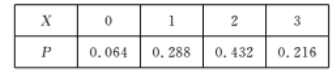
![]()
![]() .
.

 ���Ŀ��ּ�����ҵ�����ҵ����������ϵ�д�
���Ŀ��ּ�����ҵ�����ҵ����������ϵ�д� ����ѵ��ϵ�д�
����ѵ��ϵ�д�����Ŀ��ij�����һ������7��10���ĸ������±�
����� | 7 | 8 | 9 | 10 |
����� | 0.16 | 0.19 | 0.28 | 0.24 |
��������������һ�� ����У�
��1������10����9���ĸ��ʣ�
��2����������7���ĸ��ʣ�
��3�����л�������8���ĸ��ʣ�