题目内容
【题目】已知函数y=1﹣3sinx
(1)画出上述函数的图象
(2)求上述函数的最大值、最小值和周期,并求这个函数取最大值、最小值的x值的集合.
【答案】
(1)解:列表为:
x | 0 | | π | | 2π |
sinx | 0 | 1 | 0 | ﹣1 | 0 |
y=1﹣3sinx | 1 | ﹣2 | 1 | 4 | 1 |
画出图形,如图:
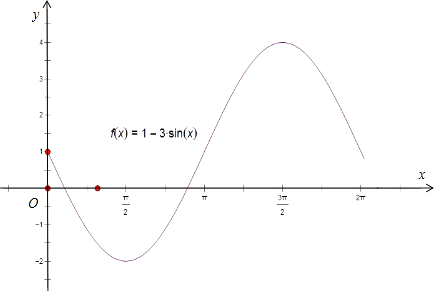
(2)解:∵﹣1≤sinx≤1,
∴函数y=1﹣3sinx的最大值是4,最小值是﹣2,周期为2π,
当y取最大值时x的集合为{x|x= ![]() +2kπ,k∈Z}.
+2kπ,k∈Z}.
当y取最小值时x的集合为{x|x= ![]() +2kπ,k∈Z}
+2kπ,k∈Z}
【解析】(1)根据五点做出函数的简图,即可得到结论.(2)根据正弦函数的图象与性质作答.
【考点精析】掌握正弦函数的奇偶性和五点法作函数y=Asin(ωx+φ)的图象是解答本题的根本,需要知道正弦函数为奇函数;描点法及其特例—五点作图法(正、余弦曲线),三点二线作图法(正、余切曲线).

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】某人射击一次命中7~10环的概率如下表
命中环数 | 7 | 8 | 9 | 10 |
命中概率 | 0.16 | 0.19 | 0.28 | 0.24 |
计算这名射手在一次 射击中:
(1)射中10环或9环的概率;
(2)至少射中7环的概率;
(3)射中环数不足8环的概率.