题目内容
【题目】已知函数f(x)=x|x-4| (x∈R)
(1)用分段形式写出函数f(x)的表达式，并作出函数f(x)的图象;
(2) 根据图象指出f(x)的单调区间,并写出不等式f(x)>0的解集;
(3) 若h(x)=f(x)-k有三个零点,写出k的取值范围.
【答案】（1）见解析；（2）见解析；（3）
【解析】
分析：（1）根据绝对值的定义，利用零点分段法，分当
时和当
时两种情况，化简函数的解析式，最后可将函数
写出分段函数的形式；根据分段函数图象分段画的原则，结合二次函数的图象和性质，可作出图象；
（2）结合图象可得函数的单调区间及不等式
的解集;；
（3）根据（2）中函数的图象，结合函数的极大值为0，极小值为-4，可得
有三个零点时
的取值范围．
详解：
（1）
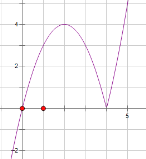当时
，，
当时
，
综上所述：
；根据分段函数图象的作法，其函数图象如图所示：
（2）单调增区间:
单调减区间:
、
不等式解集为：
；
（3）写出的取值范围是:
练习册系列答案
相关题目
【题目】（Ⅰ）如表所示是某市最近5年个人年平均收入表节选．求y关于x的回归直线方程，并估计第6年该市的个人年平均收入（保留三位有效数字）．
年份x | 1 | 2 | 3 | 4 | 5 |
收入y（千元） | 21 | 24 | 27 | 29 | 31 |
其中
，
，
附1：
= ，=﹣
（Ⅱ）下表是从调查某行业个人平均收入与接受专业培训时间关系得到2×2列联表：
受培时间一年以上 | 受培时间不足一年 | 总计 | |
收入不低于平均值 | 60 | 20 | |
收入低于平均值 | 10 | 20 | |
总计 | 100 |
完成上表，并回答：能否在犯错概率不超过0.05的前提下认为“收入与接受培训时间有关系”．
附2：
P（K2≥k0） | 0.50 | 0.40 | 0.10 | 0.05 | 0.01 | 0.005 |
k0 | 0.455 | 0.708 | 2.706 | 3.841 | 6.635 | 7.879 |
附3：
K2=．（n=a+b+c+d）
