题目内容
2.设e1、e2分别为具有公共焦点F1、F2的椭圆和双曲线的离心率,P是两曲线的一个公共点,且满足|$\overrightarrow{PF}$1+$\overrightarrow{PF}$2|=|$\overrightarrow{{F}_{1}{F}_{2}}$|,则$\frac{{e}_{1}{e}_{2}}{\sqrt{{e}_{1}^{2}+{e}_{2}^{2}}}$=$\frac{\sqrt{2}}{2}$.分析 设出椭圆的长半轴,双曲线的实半轴,它们的半焦距,利用椭圆的和双曲线的定义可得焦半径,写出两个曲线的离心率,即可得到结果.
解答 解:设椭圆的长半轴是a1,双曲线的实半轴是a2,它们的半焦距都是c.
并设|PF1|=m,|PF2|=n,m>n,
根据椭圆的和双曲线的定义可得m+n=2a1,m-n=2a2,解得m=a1+a2,n=a1-a2.
∵设椭圆的长半轴是a1,双曲线的实半轴是a2,它们的半焦距是c.
并设|PF1|=m,|PF2|=n,m>n,
根据椭圆的和双曲线的定义可得m+n=2a1,m-n=2a2,解得m=a1+a2,n=a1-a2,
∵|$\overrightarrow{PF}$1+$\overrightarrow{PF}$2|=|$\overrightarrow{{F}_{1}{F}_{2}}$|,即2|PO|=2|OF2|,故△PF1F2 为直角三角形,∴PF1⊥PF2,
由勾股定理得|PF1|2+|PF2|2=|F1F2|2 ,可得(a1+a2)2+(a1-a2)2=(2c)2,
化简可得a12+a22=2c2,∴$\frac{1}{{{e}_{1}}^{2}}$+$\frac{1}{{{e}_{2}}^{2}}$=2,
∴$\frac{{e}_{1}{e}_{2}}{\sqrt{{e}_{1}^{2}+{e}_{2}^{2}}}$=$\sqrt{\frac{1}{\frac{1}{{{e}_{1}}^{2}}+\frac{1}{{{e}_{2}}^{2}}}}$=$\frac{1}{\sqrt{2}}$=$\frac{\sqrt{2}}{2}$,
故答案为:$\frac{\sqrt{2}}{2}$.
点评 本题考查圆锥曲线的共同特征,解题的关键是运用椭圆和双曲线的定义得到两个曲线的参数之间的关系,属于中档题.

| A. | (-∞,+∞) | B. | (-∞,0) | C. | (0,+∞) | D. | (1,+∞) |
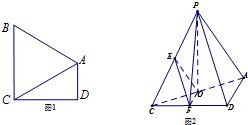 如图1,在直角梯形ABCD中,AD∥BC,∠ADC=90°,BA=BC=AC=2,把△BAC沿AC折起到△PAC的位置,使得P点在平面ADC上的正投影O恰好落在线段AC上,如图2所示.点E,F分别为棱PC,CD的中点.
如图1,在直角梯形ABCD中,AD∥BC,∠ADC=90°,BA=BC=AC=2,把△BAC沿AC折起到△PAC的位置,使得P点在平面ADC上的正投影O恰好落在线段AC上,如图2所示.点E,F分别为棱PC,CD的中点.