题目内容
【题目】(1)求经过点P(4,1),且在两坐标轴上的截距相等的直线方程.
(2)设直线y=x+2a与圆C:x2+y2-2ay-2=0相交于A,B两点,若|AB|=2![]() ,求圆C的面积.
,求圆C的面积.
【答案】(1)x-4y=0或x+y-5=0.(2)4π
【解析】
(1)设直线l在x,y轴上的截距均为a,分a=0和a≠0两种情况分别求出直线l的方程.
(2)由圆的方程得到圆心坐标和半径r,由垂径定理得到圆心到直线的距离,解出a值,则面积可求
(1)设直线l在x,y轴上的截距均为a,若a=0,即l过点(0,0)和(4,1),
∴l的方程为y=![]() x,即x-4y=0.
x,即x-4y=0.
若a≠0,则设l的方程为![]() ,∵l过点(4,1),∴
,∵l过点(4,1),∴![]() =1,
=1,
∴a=5,∴l的方程为x+y-5=0.
综上可知,直线l的方程为x-4y=0或x+y-5=0.
(2)圆C:x2+y2-2ay-2=0,即C:x2+(y-a)2=a2+2,圆心为C(0,a),半径r=![]() ,
,
C到直线y=x+2a的距离为d=![]() =
=![]() .
.
又由|AB|=2![]() ,得
,得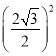 +
+ =a2+2,解得a2=2,所以圆的面积为π(a2+2)=4π.
=a2+2,解得a2=2,所以圆的面积为π(a2+2)=4π.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
相关题目

