题目内容
6. 如图所示,在四棱锥P-ABCD中,PA⊥底面 ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点,证明:
如图所示,在四棱锥P-ABCD中,PA⊥底面 ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点,证明:(1)AE⊥CD
(2)PD⊥平面ABE.
分析 (1)由PA⊥底面ABCD,可得 CD⊥PA,又CD⊥AC,故CD⊥面PAC,从而证得CD⊥AE.
(2)由等腰三角形的底边中线的性质可得AE⊥PC,由(1)知CD⊥AE,从而AE⊥面PCD,AE⊥PD,再由AB⊥PD 可得 PD⊥面ABE.
解答 证明:(1)PA⊥底面ABCD,
∴CD⊥PA.
又CD⊥AC,PA∩AC=A,
∴CD⊥面PAC,AE?面PAC,
∴CD⊥AE.
(2)PA=AB=BC,∠ABC=60°,
∴PA=AC,E是PC的中点,
∴AE⊥PC,
由(1)知CD⊥AE,从而AE⊥面PCD,
∴AE⊥PD.
∵PA⊥底面 ABCD,可得AB⊥PA,又AB⊥AD,PA∩AD=A,
∴AB⊥平面PAD,
∴易知BA⊥PD,
∴PD⊥面ABE.
点评 本题主要考查了直线与平面垂直的判定,空间中直线与直线之间的位置关系,考查了空间想象能力和推理论证能力,属于中档题.

练习册系列答案
相关题目
18.设集合A={x|2<x<5},B={x|x<b},若A⊆B,则b的取值范围是( )
| A. | b≤2 | B. | b≤5 | C. | b≥2 | D. | b≥5 |
15.直线2x-y-10=0和圆(x-2)2+(y+1)2=3的位置关系是( )
| A. | 相离 | B. | 相切 | C. | 相交但不过圆心 | D. | 过圆心 |
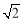 ,
, ,
, ,
, ,
, ,……,则
,……,则 是这个数列的第( )项
是这个数列的第( )项 如图,四边形ABCD是梯形,四边形CDEF是矩形,且平面ABCD⊥平面CDEF,∠BAD=∠CDA=90°,AB=AD=DE=CD=2,M是线段AE上的动点.
如图,四边形ABCD是梯形,四边形CDEF是矩形,且平面ABCD⊥平面CDEF,∠BAD=∠CDA=90°,AB=AD=DE=CD=2,M是线段AE上的动点.