题目内容
19.已知数列{an}的通项公式an=10n,n∈N+,bn=$\frac{1}{lg{a}_{2n-1}lg{a}_{2n+1}}$,则数列{bn}的前n项和Sn=$\frac{n}{2n+1}$.分析 通过对数的运算性质、裂项可知bn=$\frac{1}{2}$($\frac{1}{2n-1}$-$\frac{1}{2n+1}$),并项相加即得结论.
解答 解:∵an=10n,n∈N+,
∴a2n-1=102n-1,a2n+1=102n+1,
∴bn=$\frac{1}{lg{a}_{2n-1}lg{a}_{2n+1}}$
=$\frac{1}{lg1{0}^{2n-1}•lg1{0}^{2n+1}}$
=$\frac{1}{(2n-1)(2n+1)}$
=$\frac{1}{2}$($\frac{1}{2n-1}$-$\frac{1}{2n+1}$),
∴Sn=$\frac{1}{2}$(1-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{5}$+…+$\frac{1}{2n-1}$-$\frac{1}{2n+1}$)
=$\frac{1}{2}$(1-$\frac{1}{2n+1}$)
=$\frac{n}{2n+1}$,
故答案为:$\frac{n}{2n+1}$.
点评 本题考查数列的通项及前n项和,考查运算求解能力,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
9.设集合A={x|x≤2},则下列四个关系中正确的是( )
| A. | 1∈A | B. | 1∉A | C. | {1}∈A | D. | 1⊆A |
 中,内角
中,内角 ,
,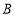 ,
, 所对的边分别为
所对的边分别为 ,
, ,
, ,且
,且 边上的高为
边上的高为 ,则
,则 的最大值为( )
的最大值为( ) B.
B.
 D.4
D.4