题目内容
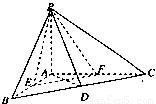
如图,在三棱锥P-ABC中,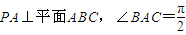 ,PA=2,AB=AC=4,点D、E、F分别为BC、AB、AC的中点.
,PA=2,AB=AC=4,点D、E、F分别为BC、AB、AC的中点.(I)求证:EF⊥平面PAD;
(II)求点A到平面PEF的距离;
(III)求二面角E-PF-A的大小.
【答案】分析:(I)欲证EF⊥平面PAD,根据直线与平面垂直的判定定理可知只需证EF与平面PAD内两相交直线垂直,而PA⊥EF,EF⊥AD,PA∩AD=A,满足定理的条件;
(II)设EF与AD相交于点G,连接PG,过A做AO⊥平面PEF,则O在PG上,所以线段AO的长为点A到平面PEF的距离,在三角形PAG中求出AO,即得到了点A到平面PEF的距离;
(III)过A做AH⊥PF,垂足为H,连接EH,根据二面角平面角的定义可知∠EHA为二面角E-PF-A的一个平面角,在直角三角形EHA中求出此角的正切值,最后用反三角函数表示即可.
解答:解:(I)∵PA⊥平面ABC,∴PA⊥EF,
AD为PD在平面ABC内的射影.
又∵点E、F分别为AB、AC的中点,∴EF∥BC
在△ABC中,由于AB=AC,故AD⊥BC,
所以EF⊥AD,∴PA⊥EF,EF⊥AD
∴EF⊥平面PAD(4分)
(II)设EF与AD相交于点G,连接PG.
∵EF⊥平面PAD,∴面PEF⊥dmPAD,交线为PG,
过A做AO⊥平面PEF,则O在PG上,
所以线段AO的长为点A到平面PEF的距离
在 ,∴
,∴
即点A到平面PEF的距离为 (8分)
(8分)
(III)∵ ∴BA⊥平面PAC.
∴BA⊥平面PAC.
过A做AH⊥PF,垂足为H,连接EH.
则EH⊥PF
所以∠EHA为二面角E-PF-A的一个平面角.
在 ,∴
,∴
即二面角E-PF-A的正切值为 ∴
∴ .(12分)
.(12分)
点评:本题主要考查了直线与平面垂直的判定,以及点到平面的距离和二面角的度量,考查空间想象能力,几何逻辑推理能力,以及计算能力.
(II)设EF与AD相交于点G,连接PG,过A做AO⊥平面PEF,则O在PG上,所以线段AO的长为点A到平面PEF的距离,在三角形PAG中求出AO,即得到了点A到平面PEF的距离;
(III)过A做AH⊥PF,垂足为H,连接EH,根据二面角平面角的定义可知∠EHA为二面角E-PF-A的一个平面角,在直角三角形EHA中求出此角的正切值,最后用反三角函数表示即可.
解答:解:(I)∵PA⊥平面ABC,∴PA⊥EF,
AD为PD在平面ABC内的射影.
又∵点E、F分别为AB、AC的中点,∴EF∥BC
在△ABC中,由于AB=AC,故AD⊥BC,
所以EF⊥AD,∴PA⊥EF,EF⊥AD
∴EF⊥平面PAD(4分)
(II)设EF与AD相交于点G,连接PG.
∵EF⊥平面PAD,∴面PEF⊥dmPAD,交线为PG,
过A做AO⊥平面PEF,则O在PG上,
所以线段AO的长为点A到平面PEF的距离
在
 ,∴
,∴
即点A到平面PEF的距离为
 (8分)
(8分)(III)∵
 ∴BA⊥平面PAC.
∴BA⊥平面PAC.过A做AH⊥PF,垂足为H,连接EH.
则EH⊥PF
所以∠EHA为二面角E-PF-A的一个平面角.
在
 ,∴
,∴
即二面角E-PF-A的正切值为
 ∴
∴ .(12分)
.(12分)点评:本题主要考查了直线与平面垂直的判定,以及点到平面的距离和二面角的度量,考查空间想象能力,几何逻辑推理能力,以及计算能力.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
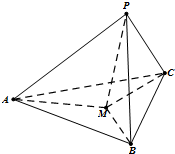 如图,在三棱锥P-ABC中,PA、PB、PC两两垂直,且PA=3.PB=2,PC=1.设M是底面ABC内一点,定义f(M)=(m,n,p),其中m、n、p分别是三棱锥M-PAB、三棱锥M-PBC、三棱锥M-PCA的体积.若f(M)=(
如图,在三棱锥P-ABC中,PA、PB、PC两两垂直,且PA=3.PB=2,PC=1.设M是底面ABC内一点,定义f(M)=(m,n,p),其中m、n、p分别是三棱锥M-PAB、三棱锥M-PBC、三棱锥M-PCA的体积.若f(M)=( 如图,在三棱锥P-ABC中,PA⊥底面ABC,∠ACB=90°,AE⊥PB于E,AF⊥PC于F,若PA=AB=2,∠BPC=θ,则当△AEF的面积最大时,tanθ的值为( )
如图,在三棱锥P-ABC中,PA⊥底面ABC,∠ACB=90°,AE⊥PB于E,AF⊥PC于F,若PA=AB=2,∠BPC=θ,则当△AEF的面积最大时,tanθ的值为( ) 如图,在三棱锥P-ABC中,PA=PB=AB=2,BC=3,∠ABC=90°,平面PAB⊥平面ABC,D、E分别为AB、AC中点.
如图,在三棱锥P-ABC中,PA=PB=AB=2,BC=3,∠ABC=90°,平面PAB⊥平面ABC,D、E分别为AB、AC中点. 如图,在三棱锥P-ABC中,已知PA=PB=PC,∠BPA=∠BPC=∠CPA=40°,一绳子从A点绕三棱锥侧面一圈回到点A的最短距离是
如图,在三棱锥P-ABC中,已知PA=PB=PC,∠BPA=∠BPC=∠CPA=40°,一绳子从A点绕三棱锥侧面一圈回到点A的最短距离是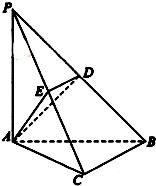 如图,在三棱锥P-ABC中,PA⊥底面ABC,∠BCA=90°,AP=AC,点D,E分别在棱
如图,在三棱锥P-ABC中,PA⊥底面ABC,∠BCA=90°,AP=AC,点D,E分别在棱