题目内容
5.已知a,b,c分别是△ABC的三个内角A,B,C所对的边,若a=$\sqrt{3}$,b=1,cosC=$\frac{\sqrt{3}}{3}$,则sinB=$\frac{\sqrt{3}}{3}$.分析 由题意和余弦定理可得c值,由同角三角函数基本关系可得sinC=$\frac{\sqrt{6}}{3}$,由正弦定理得sinB=$\frac{bsinC}{c}$,代值计算可得.
解答 解:由题意和余弦定理可得c2=($\sqrt{3}$)2+12-2×$\sqrt{3}$×1×$\frac{\sqrt{3}}{3}$=2,
∴c=$\sqrt{2}$,∵0<C<π,cosC=$\frac{\sqrt{3}}{3}$,∴sinC=$\frac{\sqrt{6}}{3}$,
∴由正弦定理得sinB=$\frac{bsinC}{c}$=$\frac{1×\frac{\sqrt{6}}{3}}{\sqrt{2}}$=$\frac{\sqrt{3}}{3}$,
故答案为:$\frac{\sqrt{3}}{3}$.
点评 本题考查解三角形,涉及正余弦定理的综合应用,属基础题.

练习册系列答案
相关题目
20.经过坐标原点,且与圆(x-3)2+(y+1)2=2相切于第四象限的直线方程是( )
| A. | x-y=0 | B. | x+y=0 | C. | x-7y=0 | D. | x+7y=0 |
5.从某校高二年级随机抽取10名学生进行数学能力测试,成绩结果:68,81,79,81,90,86,74,84,69,78,设学生测试成绩的平均数和中位数,众数分别为a,b,c,则( )
| A. | a-b<c | B. | a<b-c | C. | a<b<c | D. | b<a<c |
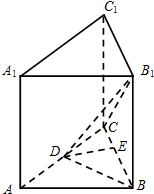 如图,直三棱柱ABC-A1B1C1中,∠BAC=$\frac{π}{2}$,D为AC中点,E为BC上一点,且∠CDE=∠ABC.
如图,直三棱柱ABC-A1B1C1中,∠BAC=$\frac{π}{2}$,D为AC中点,E为BC上一点,且∠CDE=∠ABC.