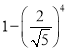��Ŀ����
����Ŀ��ij��������ˮ�����������£�ԭʼ��ˮ���Ⱦ���Aϵͳ����,���������ˮ��A��ˮ���ﵽ����������ƴ�꣩�ĸ���Ϊ![]() .��������,��ȷ�ϴ����ֱ���ŷţ����������������Bϵͳ������ֱ���ŷ�.
.��������,��ȷ�ϴ����ֱ���ŷţ����������������Bϵͳ������ֱ���ŷ�.
ij������![]() ����ˮ����A��ˮ��,�ֱ�ȡ�������. �����ˮ�������ʱ,�ȿ����������,Ҳ���Խ����ɸ����������һ����.���������ֻҪ�����������,���������Ļ������ز����.��������������,������и�������������������飻������������,��ԭˮ�ص���ˮֱ���ŷ�.
����ˮ����A��ˮ��,�ֱ�ȡ�������. �����ˮ�������ʱ,�ȿ����������,Ҳ���Խ����ɸ����������һ����.���������ֻҪ�����������,���������Ļ������ز����.��������������,������и�������������������飻������������,��ԭˮ�ص���ˮֱ���ŷ�.
�����������ַ���,
����һ��������飻
��������ƽ���ֳ����黯�飻
��������������������һ����,ʣ�µ�һ���������飻
�����ģ�����һ����.
�������������ֵԽС,����Խ���š�.
���� ��![]() ,��
,��![]() ��A��ˮ������ϻ�����������ĸ��ʣ�
��A��ˮ������ϻ�����������ĸ��ʣ�
���� ��![]() ,����
,����![]() ��A��ˮ������Ҫ����,���ʣ�����һ,��,�����ĸ���š���
��A��ˮ������Ҫ����,���ʣ�����һ,��,�����ĸ���š���
���� �������������ȡ������ġ������š�,��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
���𰸡�����![]() ;��II��������;��III��������.
;��II��������;��III��������.
���������������������������������¼��ظ������ĸ���Ϊ��������¼����ʳ˻�����������¼��ĸ��ʺ�Ϊ![]() ���ɵý�������ֱ�������ַ�����Ӧ�ֲ��У���һ��������Ե�����ֵ���Ƚ�����ֵ��С�����ŷ��������ֱ��������ֵ������������С��ϵ��������
���ɵý�������ֱ�������ַ�����Ӧ�ֲ��У���һ��������Ե�����ֵ���Ƚ�����ֵ��С�����ŷ��������ֱ��������ֵ������������С��ϵ��������![]() �IJ���ʽ�����
�IJ���ʽ�����![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
������������û���������ĸ�����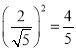 �� 2��
�� 2��
���Ը��ݶ����¼�ԭ���������ĸ���Ϊ![]() ��
��
��II������һ�������⣬������Ϊ![]() ��
��
���������ɣ�I��֪��ÿ�����������ļ��ʱ��������������Ϊ![]() ������Ϊ
������Ϊ![]() ����������������Ϊ
����������������Ϊ![]() ������Ϊ
������Ϊ![]() �� �ʷ������ļ�����
�� �ʷ������ļ�����![]() ��
�� ![]() ����ȡ
����ȡ![]() ��
�� ![]() ��
�� ![]() �����ʷֲ������£�
�����ʷֲ������£�
|
|
|
|
|
|
|
|
����÷�����������Ϊ![]() ��
��
�����ģ�����һ���⣬�Ǽ�����Ϊ![]() ��
�� ![]() ��ȡ
��ȡ![]() ��
�� ![]() �����ʷֲ������£�
�����ʷֲ������£�
|
|
|
|
|
|
����÷����ĵ�����Ϊ![]() ��
��
�ȽϿɵ�![]() ����ѡ������š���
����ѡ������š���
��III���⣺���������軯�����![]() ��
�� ![]() ��ȡ
��ȡ![]() ��
�� ![]() ��
��
|
|
|
|
|
|
![]() ��
��
�����ģ��軯�����![]() ��
�� ![]() ��ȡ
��ȡ![]() ��
�� ![]() ��
��
|
|
|
|
|
|
![]() ��
��
�������![]()
![]() ��
��
�ʵ�![]() ʱ���������ȷ����ĸ���������
ʱ���������ȷ����ĸ���������

 �Ƹ�С״Ԫ�������������ϵ�д�
�Ƹ�С״Ԫ�������������ϵ�д� ����һ������ܼƻ�ϵ�д�
����һ������ܼƻ�ϵ�д�����Ŀ����������ˮƽ����ߣ����ǶԿ���������Ҫ��Խ��Խ�ߣ�ij����Ϊ�˽�ڶԡ��������С���̬�ȣ�������![]() ��,����������������������Ƴ��±���
��,����������������������Ƴ��±���
���䣨�꣩ |
|
|
|
|
|
Ƶ�� |
|
|
|
|
|
������ |
|
|
|
|
|
��1����ɱ�������Ա�����Ƶ�ʷֲ�ֱ��ͼ����������Ա�г���̬����Ա��ƽ������ԼΪ�����ꣿ
��2������������![]() �ı�������Ա�и����ѡȡ
�ı�������Ա�и����ѡȡ![]() �˽��е���.��д�����еĻ����~��,����ѡȡ
�˽��е���.��д�����еĻ����~��,����ѡȡ![]() ����ǡ��
����ǡ��![]() �˳ֲ���̬�ȵĸ���.
�˳ֲ���̬�ȵĸ���.

����Ŀ��ij�ֲ�Ʒ��������������ָ��ֵ����������������ָ��ֵ���ֵȼ����±���
����ָ��ֵ |
|
|
|
�ȼ� | ����Ʒ | ����Ʒ | һ��Ʒ |
��ij��ҵ���������ֲ�Ʒ�г�ȡ200��������õ����µ�Ƶ�ʷֲ�ֱ��ͼ��
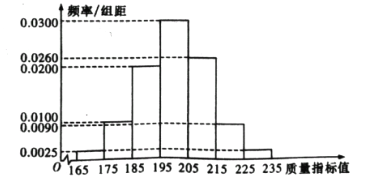
��1���������ϳ����������� ���ܷ���Ϊ����ҵ���������ֲ�Ʒ���ϡ�һ������Ʒ����Ҫռȫ����Ʒ90%���Ĺ涨��
��2���������У�����Ʒ�ȼ��÷ֲ�����ķ�����ȡ8�����ٴ���8����Ʒ�������ȡ4�������ȡ��4����Ʒ�У�һ����������Ʒ���еĸ��ʣ�
��3������ҵΪ��߲�Ʒ��������չ�ˡ����������¡��������ٳ�����⣬��Ʒ����ָ��ֵ![]() ��������
��������![]() �������������¡���������ָ��ֵ�ľ�ֵ�Ȼǰ��Լ�����˶��٣�
�������������¡���������ָ��ֵ�ľ�ֵ�Ȼǰ��Լ�����˶��٣�