题目内容
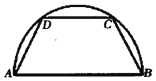
【题目】如图，将一半径为2的半圆形纸板裁剪成等腰梯形ABCD的形状，下底AB是半圆的直径，上底CD的端点在圆周上，则所得梯形面积的最大值为（ ）
A. 3
B. 3
C. 5
D. 5
【答案】A
【解析】解：连接OD，过C，D分别作DE⊥AB于E，CF⊥AB，垂足分别为E，F．
设∠AOD=θ，θ∈
．
OE=2cosθ，DE=2sinθ．
可得CD=2OE=4cosθ，
∴梯形ABCD的面积S=
（4+4cosθ）2sinθ
=4sinθ（1+cosθ），
S′=4（cosθ+cos2θ﹣sin2θ）
=4（2cos2θ+cosθ﹣1）
=4（2cosθ﹣1）（cosθ+1）．
∵θ∈
．∴cosθ∈（0，1）．
∴当cosθ=
即θ=
时，S取得最大值，S=3
．
故选：A．
【题目】某花店每天以每枝5元的价格从农场购进若干枝玫瑰花，然后以每枝10元的价格出售，如果当天卖不完，剩下的玫瑰花作垃圾处理．
（1）若花店一天购进16枝玫瑰花，求当天的利润y（单位：元）关于当天需求量n（单位：枝，n∈N）的函数解析式．
（2）花店记录了100天玫瑰花的日需求量（单位：枝），整理得下表：
日需求量n | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
频数 | 10 | 20 | 16 | 16 | 15 | 13 | 10 |
以100天记录的各需求量的频率作为各需求量发生的概率．
（i）若花店一天购进16枝玫瑰花，X表示当天的利润（单位：元），求X的分布列，数学期望及方差；
（ii）若花店计划一天购进16枝或17枝玫瑰花，你认为应购进16枝还是17枝？请说明理由．
【题目】某种零件按质量标准分为1，2，3，4，5五个等级，现从一批该零件巾随机抽取20个，对其等级进行统计分析，得到频率分布表如下
等级 | 1 | 2 | 3 | 4 | 5 |
频率 | 0.05 | m | 0.15 | 0.35 | n |
（1）在抽取的20个零件中，等级为5的恰有2个，求m，n；
（2）在（1）的条件下，从等级为3和5的所有零件中，任意抽取2个，求抽取的2个零件等级恰好相同的概率．
