题目内容
下列函数中,在其定义域是减函数的是( )
A. | B. |
C. | D. |
D
解析试题分析: 是二次函数,在定义域内有增有减;
是二次函数,在定义域内有增有减; 的定义域是
的定义域是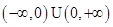 ,但它在
,但它在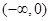 和
和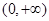 分别单调递减,在定义域内不是单调递减的;根据复合函数的单调性值
分别单调递减,在定义域内不是单调递减的;根据复合函数的单调性值 在
在 上单调递增,在
上单调递增,在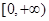 上单调递减;只有
上单调递减;只有 在定义域上单调递减.
在定义域上单调递减.
考点:本小题主要考查函数单调性的判断,考查学生的逻辑推理能力.
点评:要注意函数的单调性是区间定义,它可以有几个单调区间,但在定义域上不是单调的,另外牢固掌握基本初等函数的单调性可以帮助解决此类问题.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
函数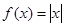 和
和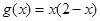 的递增区间依次是( )
的递增区间依次是( )
A.(-∞,0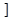 ,(-∞,1 ,(-∞,1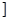 | B.(-∞,0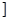 ,[1,+∞ ,[1,+∞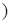 |
C.[0,+∞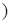 ,(-∞,1 ,(-∞,1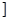 | D.[0,+∞),[1,+∞) |
已知 是偶函数,它在[0,+∞)上是减函数,若
是偶函数,它在[0,+∞)上是减函数,若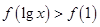
 ,则
,则 的取值范围是( )
的取值范围是( )
A. | B. |
C. | D. |
若函数 唯一的零点在区间(1,3)、(1,4)、(1,5)内,那么下列命题中错误的是( )
唯一的零点在区间(1,3)、(1,4)、(1,5)内,那么下列命题中错误的是( )
A.函数 在(1,2)或 在(1,2)或 内有零点 内有零点 | B.函数 在(3,5)内无零点 在(3,5)内无零点 |
C.函数 在(2,5)内有零点 在(2,5)内有零点 | D.函数 在(2,4)内不一定有零点. 在(2,4)内不一定有零点. |
若f (lnx)=3x+4,则f (x)的表达式为
| A.3lnx | B.3lnx+4 |
| C.3ex | D.3ex+4 |
定义在R上的函数 满足
满足 ,且
,且
 .若当
.若当 时不等式
时不等式 成立,则
成立,则 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
将函数 在
在 上的所有极值点按从小到大排成一列
上的所有极值点按从小到大排成一列 ,给出以下不等式: ①
,给出以下不等式: ① ; ②
; ② ;③
;③ ;④
;④ ;其中,正确的判断是( )
;其中,正确的判断是( )
| A.①③ | B.①④ | C.②③ | D.②④ |
 ;②
;② ;③
;③ ;④
;④ .则下列函数图象(在第一象限部分)从左到右依次与函数序号的正确对应顺序是
.则下列函数图象(在第一象限部分)从左到右依次与函数序号的正确对应顺序是 
 的图象为
的图象为