题目内容
若f (lnx)=3x+4,则f (x)的表达式为
| A.3lnx | B.3lnx+4 |
| C.3ex | D.3ex+4 |
D.
解析试题分析:设t=lnx,则x=et,t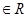 ,所以f(t)=3et+4,即f(x)= 3ex+4.
,所以f(t)=3et+4,即f(x)= 3ex+4.
考点:本题考查函数解析式的求法;指数式与对数式的互化。
点评:若已知复合函数f[g(x)]的解析式,求函数f(x)的解析式,常用换元法。令g(x)=" t" ,求f(t)的解析式,然后t换为x即可。 但要注意换元后,应再求新变量的取值范围,即为函数的定义域。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若一系列函数的解析式相同,值域相同,但定义域不同,则称这些函数为“孪生函数”,那么函数解析式为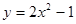 ,值域为
,值域为 的“孪生函数”共有( )
的“孪生函数”共有( )
| A.10个 | B.9个 | C.8个 | D.4个 |
若函数 与
与 的定义域均为R,则( )
的定义域均为R,则( )
| A.f(x)与g(x)均为偶函数 | B.f(x)为偶函数,g(x)为奇函数 |
| C.f(x)与g(x)均为奇函数 | D.f(x)为奇函数,g(x)为偶函数 |
下列函数中,值域为(0, )的函数是( )
)的函数是( )
A. | B. | C. | D. |
下列函数中,在其定义域是减函数的是( )
A. | B. |
C. | D. |
下列函数中与函数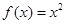 相等的是( )
相等的是( )
A. | B. |
C. | D.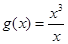 |
下列函数中是奇函数的是( )
A. | B. | C. | D. |
 在
在 上既是奇函数,又是减函数,则
上既是奇函数,又是减函数,则 的图象是( )
的图象是( )
 的图象大致是( )
的图象大致是( )