题目内容
将函数 在
在 上的所有极值点按从小到大排成一列
上的所有极值点按从小到大排成一列 ,给出以下不等式: ①
,给出以下不等式: ① ; ②
; ② ;③
;③ ;④
;④ ;其中,正确的判断是( )
;其中,正确的判断是( )
| A.①③ | B.①④ | C.②③ | D.②④ |
D
解析试题分析::∵函数f(x)=xsinx,∴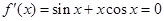 ,∴tanx=-x,
,∴tanx=-x,
∴函数f(x)在(0,+∞)内的全部极值点就是函数y=tanx与y=-x的交点的横标,
观察两条直线的交点,从纵轴向右,在每一个周期上都有一个交点,
且从左向右,交点的位置依次更靠近渐近线,
∴两个交点之间的横标之差小于一个周期,大于半个周期,故选C.
考点: 数列与三角的综合考查,导数在三角函数中的应用,正切函数的图像与性质.
点评:解本题的关键是根据导数等于零,得到tanx=-x,从而确定函数f(x)在(0,+∞)内的全部极值点就是函数y=tanx与y=-x的交点的横标,然后观察两线的交点,在每一个周期上都有一个交点,且从左向右,交点的位置更靠近渐近线,两个点之间的横标的差.

练习册系列答案
相关题目
下列函数中,在其定义域是减函数的是( )
A. | B. |
C. | D. |
函数 的单减区间是( )
的单减区间是( )
A. | B. | C. | D. |
下列函数中是奇函数的是( )
A. | B. | C. | D. |
下列函数与 有相同图象的一个函数是( )
有相同图象的一个函数是( )
A.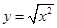 | B. |
C.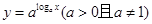 | D. |
已知 是定义在
是定义在 上的奇函数,当
上的奇函数,当 时,
时, ,则在
,则在 上
上 的表达式为
的表达式为
A. | B. | C. | D. |
设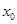 是方程
是方程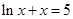 的解,则
的解,则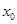 属于区间( ).
属于区间( ).
| A.(0,1) | B.(1,2) | C.(2,3) | D.(3,4) |
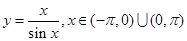 的图象可能是下列图象中的 ( )
的图象可能是下列图象中的 ( )

 的图象是曲线OAB,其中点O、A、B的坐标分别是(0,0),(1,2),(3,1),则
的图象是曲线OAB,其中点O、A、B的坐标分别是(0,0),(1,2),(3,1),则 的值是
的值是