题目内容
函数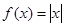 和
和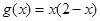 的递增区间依次是( )
的递增区间依次是( )
A.(-∞,0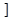 ,(-∞,1 ,(-∞,1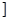 | B.(-∞,0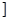 ,[1,+∞ ,[1,+∞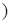 |
C.[0,+∞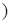 ,(-∞,1 ,(-∞,1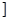 | D.[0,+∞),[1,+∞) |
C
解析试题分析:因为对于函数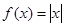 ,关于直线x=0对称,是一个偶函数,且在y轴左侧是递减的,右侧是递增的。而对于函数
,关于直线x=0对称,是一个偶函数,且在y轴左侧是递减的,右侧是递增的。而对于函数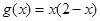 ,开口向下,对称轴为x=1,那么可知在(-∞,1
,开口向下,对称轴为x=1,那么可知在(-∞,1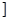 函数递增区间,因此可知选C.
函数递增区间,因此可知选C.
考点:本题主要是考查函数的单调性的求解和运用。
点评:解决该试题的关键是利用绝对值函数和二次函数的性质,分别得到函数的递增区间的求解运用。

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
函数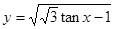 的定义域是
的定义域是
A.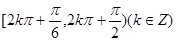 | B.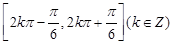 |
C.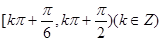 | D.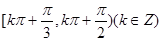 |
若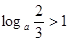 ,则a的取值范围是( )
,则a的取值范围是( )
A.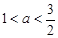 | B.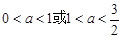 |
C.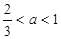 | D.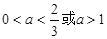 |
若一系列函数的解析式相同,值域相同,但定义域不同,则称这些函数为“孪生函数”,那么函数解析式为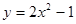 ,值域为
,值域为 的“孪生函数”共有( )
的“孪生函数”共有( )
| A.10个 | B.9个 | C.8个 | D.4个 |
函数y= 的值域是[-2,2],则函数y=
的值域是[-2,2],则函数y=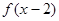 的值域是( )
的值域是( )
| A.[-2,2] | B.[-4,0] | C.[0,4] | D.[-1,1] |
设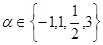 ,则使函数
,则使函数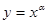 的定义域为
的定义域为 且为奇函数的所有
且为奇函数的所有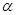 的值为( )
的值为( )
| A.1,3 | B.-1,1 | C.-1,3 | D.-1,1,3 |
下列函数中,在其定义域是减函数的是( )
A. | B. |
C. | D. |
 是定义在
是定义在 上的偶函数,在
上的偶函数,在 上是减函数,且
上是减函数,且 ,则使得
,则使得 的
的 的取值范围是( )
的取值范围是( )



 的图象只可能是 ( )
的图象只可能是 ( )