题目内容
等差数列{an}的前n项和为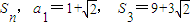 .
.(1)求数列{an}的通项an与前n项和Sn;
(2)设
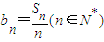 ,数列{bn}中是否存在不同的三项能成为等比数列.若存在则求出这三项,若不存在请证明.
,数列{bn}中是否存在不同的三项能成为等比数列.若存在则求出这三项,若不存在请证明.
【答案】分析:(1)由题意可得:d=2,进而得到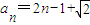 ,
,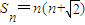 .
.
(2)由(1)得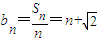 .假设数列{bn}中存在三项bp、bq、br(p、q、r互不相等)成等比数列,
.假设数列{bn}中存在三项bp、bq、br(p、q、r互不相等)成等比数列,
则bq2=bpbr,结合题意可得p=r,与p≠r矛盾.
解答:解:(1)由已知得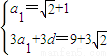
∴d=2
故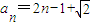 ,
,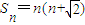
(2)由(1)得 .
.
假设数列{bn}中存在三项bp、bq、br(p、q、r互不相等)成等比数列,
则bq2=bpbr,
即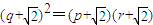 ,
,
∴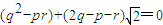
∵p,q,r∈N*,∴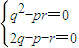
∴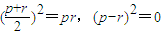 ,∴p=r
,∴p=r
与p≠r矛盾.
所以数列{bn}中任意不同的三项都不可能成等比数列.
点评:本题考查数列求通项公式与求法和,解题时要注意反证推理的合理运用.
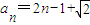 ,
,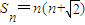 .
.(2)由(1)得
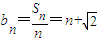 .假设数列{bn}中存在三项bp、bq、br(p、q、r互不相等)成等比数列,
.假设数列{bn}中存在三项bp、bq、br(p、q、r互不相等)成等比数列,则bq2=bpbr,结合题意可得p=r,与p≠r矛盾.
解答:解:(1)由已知得
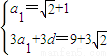
∴d=2
故
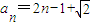 ,
,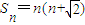
(2)由(1)得
 .
.假设数列{bn}中存在三项bp、bq、br(p、q、r互不相等)成等比数列,
则bq2=bpbr,
即
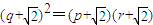 ,
,∴
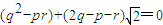
∵p,q,r∈N*,∴
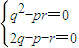
∴
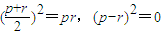 ,∴p=r
,∴p=r与p≠r矛盾.
所以数列{bn}中任意不同的三项都不可能成等比数列.
点评:本题考查数列求通项公式与求法和,解题时要注意反证推理的合理运用.

练习册系列答案
 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
设等差数列{an}的前n项和为Sn,则a5+a6>0是S8≥S2的( )
| A、充分而不必要条件 | B、必要而不充分条件 | C、充分必要条件 | D、既不充分也不必要条件 |