题目内容
14．函数y=$5\sqrt{x-1}+\sqrt{2}•\sqrt{5-x}$最大值为（ ）| A． | 108 | B． | $6\sqrt{3}$ | C． | 10 | D． | 27 |
分析 运用柯西不等式（ac+bd）2≤（a2+b2）（c2+d2），当且仅当bc=ad取得等号，变形即可得到所求的最大值．
解答 解：由柯西不等式（ac+bd）2≤（a2+b2）（c2+d2），
可得y=5$\sqrt{x-1}$+$\sqrt{2}$•$\sqrt{5-x}$≤$\sqrt{（{5}^{2}+（\sqrt{2}）^{2}）（x-1+5-x）}$
=$\sqrt{108}$=6$\sqrt{3}$，
当且仅当5$\sqrt{5-x}$=$\sqrt{2}$•$\sqrt{x-1}$，即为x=$\frac{127}{27}$时，取得最大值6$\sqrt{3}$．
故选：B．
点评 本题考查函数的最值的求法，注意运用柯西不等式，考查运算能力，属于中档题．
练习册系列答案
相关题目
4．设函数f′（x）是奇函数f（x）（x∈R）的导函数，f（3）=0，当x＜0时，xf′（x）+f（x）＞0，则有（ ）
| A． | f（-3）＜f（1）＜f（2） | B． | f（2）＜f（-3）＜f（1） | C． | f（1）＜f（-3）＜f（2） | D． | f（-3）＜f（2）＜f（1） |
5．在棱长为1的正方体ABCD-A1B1C1D1中，M和N分别为A1B1和BB1的中点，那么与直线AM垂直的向量有（ ）
| A． | $\overrightarrow{CN}$ | B． | $\overrightarrow{BC}$ | C． | $\overrightarrow{C{C}_{1}}$ | D． | $\overrightarrow{{B}{C}_{1}}$ |
9．二项式（x3-$\frac{1}{{x}^{2}}$）5的展开式中的常数项为（ ）
| A． | 10 | B． | -10 | C． | -14 | D． | 14 |
19．已知等差数列的首项为a1，公差为d．则该数列的通项公式为（ ）
| A． | an=a1+d（n+1） | B． | an=a1+dn | C． | an=a1+d（n-1） | D． | an=a1+d（n-2） |
6．
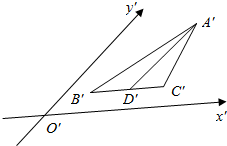如图所示的水平放置的三角形的直观图中，D′是△A′B′C′中B′C′边的中点，那么A′B′，A′D′，A′C′三条线段对应原图形中线段AB，AD，AC中（ ）
如图所示的水平放置的三角形的直观图中，D′是△A′B′C′中B′C′边的中点，那么A′B′，A′D′，A′C′三条线段对应原图形中线段AB，AD，AC中（ ）| A． | 最长的是AB，最短的是AC | B． | 最长的是AC，最短的是AB | ||
| C． | 最长的是AB，最短的是AD | D． | 最长的是AD，最短的是AC |
4．非零向量 $\overrightarrow{a}$，$\overrightarrow{b}$夹角为120°，且|$\overrightarrow{a}$-$\overrightarrow{b}$|=2，则|$\overrightarrow{a}$+$\overrightarrow{b}$|的取值范围为（ ）
| A． | [1，$\sqrt{3}$] | B． | [2，$\frac{4\sqrt{3}}{3}$] | C． | [$\frac{2\sqrt{3}}{3}$，4） | D． | [1，2] |