题目内容
20.直线$\left\{\begin{array}{l}{x={x}_{0}+t}\\{y={y}_{0}-\sqrt{3}t}\end{array}\right.$(t为参数)上任意一点P到P0(x0,y0)的距离为2|t|.分析 直线$\left\{\begin{array}{l}{x={x}_{0}+t}\\{y={y}_{0}-\sqrt{3}t}\end{array}\right.$上的任意一点可表示为(x0+t,y0-$\sqrt{3}$t),由两点间的距离公式可得答案.
解答 解:直线$\left\{\begin{array}{l}{x={x}_{0}+t}\\{y={y}_{0}-\sqrt{3}t}\end{array}\right.$上的任意一点可表示为(x0+t,y0-$\sqrt{3}$t),
由两点间的距离公式可得d=$\sqrt{({x}_{0}+t-{x}_{0})^{2}+({y}_{0}-\sqrt{3}t-{y}_{0})^{2}}$=$\sqrt{4{t}^{2}}$=2|t|
故答案为:2|t|
点评 本题考查直线的参数方程和两点间的距离公式,属基础题.

练习册系列答案
相关题目
15.从-1、0、1、2这四个数中选出三个不同的数作为二次函数f(x)=ax2+bx+c的系数组成不同的二次函数,其中使二次函数有变号零点的概率为( )
| A. | $\frac{7}{9}$ | B. | $\frac{7}{12}$ | C. | $\frac{5}{9}$ | D. | $\frac{5}{12}$ |
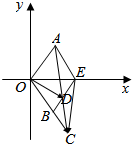 如图所示,△AOE和△BOE都是边长为1的等边三角形,延长OB到C,使|BC|=t|OB|(t>0),连接AC交BE于D,
如图所示,△AOE和△BOE都是边长为1的等边三角形,延长OB到C,使|BC|=t|OB|(t>0),连接AC交BE于D,