题目内容
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,又数列
,又数列![]() 满足:
满足: ![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)当![]() 为何值时,数列
为何值时,数列![]() 是等比数列?此时数列
是等比数列?此时数列![]() 的前
的前![]() 项和为
项和为![]() ,若存在
,若存在![]() ,使m<
,使m<![]() 成立,求
成立,求![]() 的最大值.
的最大值.
【答案】(1) 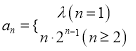 (2)
(2) ![]() ,m的最大值为1
,m的最大值为1
【解析】试题分析:(1)由数列的前n项和求出首项,再由an=Sn-Sn-1求出n≥2的通项公式,验证首项后得答案;(2)由anbn=n求出数列{bn}的通项公式,结合数列{bn}是等比数列求得λ值,求出等比数列![]() 的前
的前![]() 项和为
项和为![]() ,研究
,研究![]() 的单调性,求出
的单调性,求出![]() 的最小值即得解.
的最小值即得解.
试题解析:
(1)由![]() ,
,
当![]() 时,
时, ![]() ;当
;当![]() 时,,
时,, ![]()
故数列![]() 的通项公式为
的通项公式为 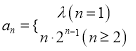
(2)由![]() ,则
,则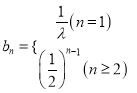 ,则数列
,则数列![]() 为等比数列,
为等比数列,
则首项为![]() 满足
满足![]() 的情况,故
的情况,故![]() ,
,
则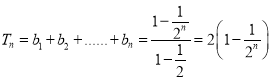
因为![]() ,所以
,所以![]() 是单调递增的,故
是单调递增的,故![]() 且
且![]()
又存在![]() ,使m<
,使m<![]() 成立,则
成立,则![]() 的最大值为1.
的最大值为1.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案
相关题目