题目内容
18. 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{{\sqrt{15}}}{4}$,F1,F2是椭圆的两个焦点,P是椭圆上任意一点,且△PF1F2的周长是8+2$\sqrt{15}$
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{{\sqrt{15}}}{4}$,F1,F2是椭圆的两个焦点,P是椭圆上任意一点,且△PF1F2的周长是8+2$\sqrt{15}$(1)求椭圆C的方程;
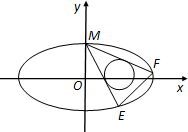
(2)设圆T:(x-t)2+y2=$\frac{4}{9}$,过椭圆的上顶点作圆T的两条切线交椭圆于E、F两点,当圆心在x轴上移动且t∈(1,3)时,求EF的斜率的取值范围.
分析 (1)由椭圆离心率得到a,c的关系,再由△PF1F2的周长是$8+2\sqrt{15}$得a,c的另一关系,联立求得a,c的值,代入隐含条件求得b,则椭圆方程可求;
(2)椭圆的上顶点为M(0,1),设过点M与圆T相切的直线方程为y=kx+1,由圆心到切线距离等于半径得到关于切线斜率的方程,由根与系数关系得到
${k}_{1}+{k}_{2}=-\frac{18t}{9{t}^{2}-4},{k}_{1}{k}_{2}=\frac{5}{9{t}^{2}-4}$,再联立一切线方程和椭圆方程,求得E的坐标,同理求得F坐标,另一两点求斜率公式得到kEF=$\frac{{{k_1}+{k_2}}}{{1-16{k_1}{k_2}}}=\frac{6t}{{28-3{t^2}}}$.然后由函数单调性求得EF的斜率的范围.
解答 解:(1)由$e=\frac{{\sqrt{15}}}{4}$,即$\frac{c}{a}=\frac{\sqrt{15}}{4}$,可知a=4b,$c=\sqrt{15}b$,
∵△PF1F2的周长是$8+2\sqrt{15}$,
∴$2a+2c=8+2\sqrt{15}$,
∴a=4,b=1,
所求椭圆方程为$\frac{x^2}{16}+{y^2}=1$;
(2)椭圆的上顶点为M(0,1),设过点M与圆T相切的直线方程为y=kx+1,
由直线y=kx+1与T相切可知$\frac{{|{kt+1}|}}{{\sqrt{{k^2}+1}}}=\frac{2}{3}$,
即(9t2-4)k2+18tk+5=0,
∴${k}_{1}+{k}_{2}=-\frac{18t}{9{t}^{2}-4},{k}_{1}{k}_{2}=\frac{5}{9{t}^{2}-4}$,
由$\left\{\begin{array}{l}y={k_1}x+1\\ \frac{x^2}{16}+{y^2}=1\end{array}\right.$,得$({1+16{k_1}^2}){x^2}+32{k_1}x=0$.
∴${x_E}=-\frac{{32{k_1}}}{{1+16{k_1}^2}}$,
同理${x_F}=-\frac{{32{k_2}}}{{1+16{k_2}^2}}$,
则${k_{EF}}=\frac{{{y_E}-{y_F}}}{{{x_E}-{x_F}}}=\frac{{({{k_1}{x_E}+1})-({{k_2}{x_F}+1})}}{{{x_E}-{x_F}}}=\frac{{{k_1}{x_E}-{k_2}{x_F}}}{{{x_E}-{x_F}}}$=$\frac{{{k_1}+{k_2}}}{{1-16{k_1}{k_2}}}=\frac{6t}{{28-3{t^2}}}$.
当1<t<3时,$f(t)=\frac{6t}{{28-3{t^2}}}$为增函数,故EF的斜率的范围为$({\frac{6}{25},18})$.
点评 本题考查了椭圆方程的求法,考查了直线与圆,直线与椭圆的位置关系,考查了直线与圆相切的条件,训练了利用函数单调性求函数的最值,是中档题.

 小学教材完全解读系列答案
小学教材完全解读系列答案 某校计划在一块空地上建造一个面积为1800m2的矩形游泳池(如图所示),它的两边都留有宽6m的休息台,顶部和底部都留有宽为3m的人行道,如何设计空地的长与宽,使所用空地的面积最小?
某校计划在一块空地上建造一个面积为1800m2的矩形游泳池(如图所示),它的两边都留有宽6m的休息台,顶部和底部都留有宽为3m的人行道,如何设计空地的长与宽,使所用空地的面积最小?