题目内容
7．解方程：log3（x-1）=log9（x+5）分析 log3（x-1）=log9（x+5），可得$lo{g}_{9}（x-1）^{2}=lo{g}_{9}（x+5）$，化为（x-1）2=x+5，x-1＞0，x+5＞0，解出即可．
解答 解：∵log3（x-1）=log9（x+5），
∴$lo{g}_{9}（x-1）^{2}=lo{g}_{9}（x+5）$，x-1＞0，x+5＞0，
∴（x-1）2=x+5，x-1＞0，x+5＞0，
解得x=4，
经过验证满足条件．
∴原方程的解为x=4．
点评 本题考查了对数方程的解法及其运算性质，考查了计算能力，属于基础题．
练习册系列答案
相关题目
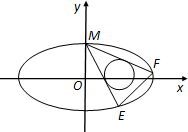已知椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b＞0}）$的离心率为$\frac{{\sqrt{15}}}{4}$，F1，F2是椭圆的两个焦点，P是椭圆上任意一点，且△PF1F2的周长是8+2$\sqrt{15}$
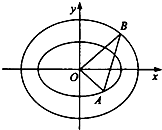如图，在平面直角坐标系xOy中，A和B分别是椭圆C1：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）和