题目内容
10.光线l从点P(1,-3)发出,被直线y=x反射后与圆(x+2)2+(y+5)2=1相切,求反射光线所在直线方程.分析 由题意易得反射关系的方程为y-1=k(x+3),由直线与圆相切可得k值,验证直线无斜率的情形即可.
解答 解:由对称性易得P(1,-3)关于直线y=x的对称点为P′(-3,1),
问题转化为从点P′射出的光线l′与圆相切,
设l′的斜率为k,则直线方程为y-1=k(x+3),即kx-y+3k+1=0,
又可得圆的圆心为(-2,-5),半径为1,
由点到直线的距离公式可得$\frac{|-2k+5+3k+1|}{\sqrt{{k}^{2}+1}}$=1,解得k=-$\frac{35}{12}$,
此时直线的方程为y-1=-$\frac{35}{12}$(x+3),即35x+12y-93=0;
当直线l′无斜率时,直线x=-3也满足题意,
∴反射光线所在直线方程为x=-3或35x+12y-93=0
点评 本题考查直线的对称性,涉及直线和圆的位置关系以及点到直线的距离公式,属中档题.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
16.已知数列{an}满足a1=0,an+1=an+2n,那么a2005的值是( )
| A. | 2003×2004 | B. | 2004×2005 | C. | 20052 | D. | 2005×2006 |
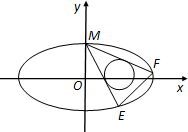 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{{\sqrt{15}}}{4}$,F1,F2是椭圆的两个焦点,P是椭圆上任意一点,且△PF1F2的周长是8+2$\sqrt{15}$
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{{\sqrt{15}}}{4}$,F1,F2是椭圆的两个焦点,P是椭圆上任意一点,且△PF1F2的周长是8+2$\sqrt{15}$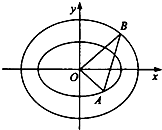 如图,在平面直角坐标系xOy中,A和B分别是椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)和
如图,在平面直角坐标系xOy中,A和B分别是椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)和 如图为一多面体ABCDFE,AB⊥AD,AB∥CD,CD=2AB=2AD=4,
如图为一多面体ABCDFE,AB⊥AD,AB∥CD,CD=2AB=2AD=4,