题目内容
9.某几何体的三视图如图所示,则该几何体的表面积为( )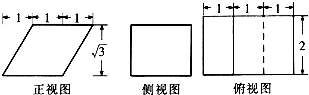
| A. | 8+2$\sqrt{3}$ | B. | 8+8$\sqrt{3}$ | C. | 12+4$\sqrt{3}$ | D. | 16+4$\sqrt{3}$ |
分析 根据几何体的三视图得出该几何体是一个斜四棱柱,AA1=2,AB=2,高为$\sqrt{3}$,画出图象,根据几何体的性质求解表面积即可.
解答 解:根据三视图得出该几何体是一个斜四棱柱,AA1=2,AB=2,高为$\sqrt{3}$,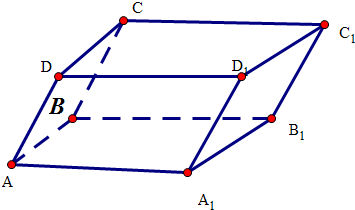
根据三视图得出侧棱长度为$\sqrt{3+1}$=2,
∴该几何体的表面积为2×(2×$\sqrt{3}$+2×2+2×2)=16$+4\sqrt{3}$,
故选:D
点评 本题考查了空间几何体的三视图,运用求解表面积,关键是恢复几何体的直观图,属于中档题.

练习册系列答案
相关题目
19.已知向量$\overrightarrow{OA}$=(3,-4)$\overrightarrow{OB}$=(6,-3),$\overrightarrow{OC}$=(2m,m+1)若$\overrightarrow{AB}$∥$\overrightarrow{OC}$,则实数m的值为( )
| A. | $\frac{3}{5}$ | B. | -$\frac{3}{5}$ | C. | 3 | D. | -3 |
4.已知A(-1,2,7),B(-3,10,-9),则线段AB中点到坐标原点的距离是( )
| A. | $\sqrt{21}$ | B. | 21 | C. | $\sqrt{41}$ | D. | 42 |
14.已知m,n都是非零实数,则“m=n”是“m2=n2”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
19.O为△ABC内一点,$\overrightarrow{AO}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AC}$,则λ+2μ-1的取值范围为( )
| A. | (-1,1) | B. | (-1,] | C. | [-1,1) | D. | [-1,1] |