题目内容
（5分）（2011•重庆）曲线y=﹣x3+3x2在点（1，2）处的切线方程为（ ）
| A．y=3x﹣1 | B．y=﹣3x+5 | C．y=3x+5 | D．y=2x |
A
解析试题分析：根据导数的几何意义求出函数f（x）在x=1处的导数，从而求出切线的斜率，再用点斜式写出切线方程，化成斜截式即可．
解：∵y=﹣x3+3x2∴y'=﹣3x2+6x，
∴y'|x=1=（﹣3x2+6x）|x=1=3，
∴曲线y=﹣x3+3x2在点（1，2）处的切线方程为y﹣2=3（x﹣1），
即y=3x﹣1，
故选A．
点评：本题主要考查了利用导数研究曲线上某点切线方程，属于基础题．
练习册系列答案
每课必练系列答案
相关题目
若
在R上可导,
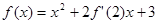,则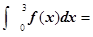
( )
A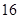． | B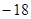． | C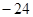． | D． |
函数
的单调递减区间为（ ）．
A． | B． | C． | D． |
若
，其中
，则
( )
A． | B． | C． | D． |
曲线
与直线
所围成的封闭图形的面积为( )
A． | B． | C． | D． |
曲线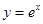
在点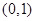
处的切线斜率为（ ）
A． | B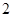． | C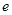． | D． |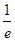
函数f(x)＝ex－x(e为自然对数的底数)在区间[－1,1]上的最大值是( )
A．1＋ | B．1 | C．e＋1 | D．e－1 |
（2011•湖北）放射性元素由于不断有原子放射出微粒子而变成其他元素，其含量不断减少，这种现象称为衰变．假设在放射性同位素铯137的衰变过程中，其含量M（单位：太贝克）与时间t（单位：年）满足函数关系：M（t）=M0
，其中M0为t=0时铯137的含量．已知t=30时，铯137含量的变化率是﹣10In2（太贝克/年），则M（60）=（ ）
| A．5太贝克 | B．75In2太贝克 | C．150In2太贝克 | D．150太贝克 |
若S1＝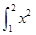
dx，S2＝
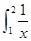dx，S3＝
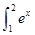dx，则S1，S2，S3的大小关系为( )
| A．S1＜S2＜S3 | B．S2＜S1＜S3 |
| C．S2＜S3＜S1 | D．S3＜S2＜S1 |