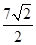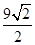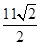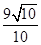题目内容
若 在R上可导,
在R上可导,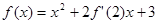 ,则
,则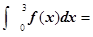 ( )
( )
A.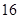 | B.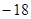 | C.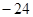 | D. |
B
解析试题分析:∵f(x)=x2+2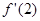 x+3,两边求导可得:
x+3,两边求导可得: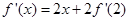 ,令x=2可得
,令x=2可得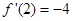 ,
,
∴f(x)=x2-8x+3,∴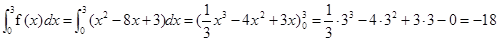 .
.
考点:导数的运用.

练习册系列答案
相关题目
定积分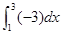 等于( )
等于( )
A.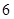 | B.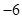 | C.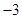 | D.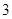 |
设函数 在
在 上可导,则
上可导,则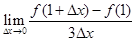 等于( )
等于( )
A.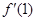 | B.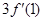 | C.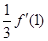 | D.以上都不对 |
已知f(x)=x3+x,若a,b,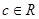 ,且a+b>0,a+c>0,b+c>0,则f(a)+f(b)+f(c)的值( )
,且a+b>0,a+c>0,b+c>0,则f(a)+f(b)+f(c)的值( )
| A.一定大于0 | B.一定等于0 |
| C.一定小于0 | D.正负都有可能 |
(5分)(2011•重庆)曲线y=﹣x3+3x2在点(1,2)处的切线方程为( )
| A.y=3x﹣1 | B.y=﹣3x+5 | C.y=3x+5 | D.y=2x |
函数y=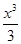 -x2+1(0<x<2)的图象上任意点处切线的倾斜角记为α,则α的最小值是( )
-x2+1(0<x<2)的图象上任意点处切线的倾斜角记为α,则α的最小值是( )
A.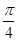 | B.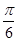 | C.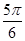 | D.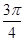 |
设f(x)=- x3+
x3+ x2+2ax,若f(x)在(
x2+2ax,若f(x)在( ,+∞)上存在单调递增区间,则实数a的取值范围为( )
,+∞)上存在单调递增区间,则实数a的取值范围为( )
A.a>- | B.a<- | C.a> | D.不存在 |
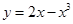 在横坐标为
在横坐标为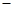 l的点处的切线为
l的点处的切线为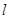 ,则点P(3,2)到直线
,则点P(3,2)到直线