题目内容
设P是椭圆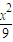 +
+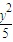 =1上一点,M,N分别是两圆:(x+2)2+y2=1和(x-2)2+y2=1上的点,则|PM|+|PN|的最小值、最大值分别为( )
=1上一点,M,N分别是两圆:(x+2)2+y2=1和(x-2)2+y2=1上的点,则|PM|+|PN|的最小值、最大值分别为( )A.4,8
B.2,6
C.6,8
D.8,12
【答案】分析:由题设知椭圆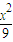 +
+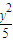 =1的焦点分别是两圆(x+2)2+y2=1和(x-2)2+y2=1的圆心,由此能求出|PM|+|PN|的最小值、最大值.
=1的焦点分别是两圆(x+2)2+y2=1和(x-2)2+y2=1的圆心,由此能求出|PM|+|PN|的最小值、最大值.
解答:解:依题意,椭圆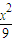 +
+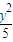 =1的焦点分别是两圆(x+2)2+y2=1和(x-2)2+y2=1的圆心,
=1的焦点分别是两圆(x+2)2+y2=1和(x-2)2+y2=1的圆心,
所以(|PM|+|PN|)max=2×3+2=8,
(|PM|+|PN|)min=2×3-2=4,
故选A.
点评:本题考查圆锥曲线的性质和应用,解题时要认真审题,仔细解答,注意公式的合理运用.
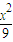 +
+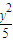 =1的焦点分别是两圆(x+2)2+y2=1和(x-2)2+y2=1的圆心,由此能求出|PM|+|PN|的最小值、最大值.
=1的焦点分别是两圆(x+2)2+y2=1和(x-2)2+y2=1的圆心,由此能求出|PM|+|PN|的最小值、最大值.解答:解:依题意,椭圆
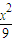 +
+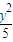 =1的焦点分别是两圆(x+2)2+y2=1和(x-2)2+y2=1的圆心,
=1的焦点分别是两圆(x+2)2+y2=1和(x-2)2+y2=1的圆心,所以(|PM|+|PN|)max=2×3+2=8,
(|PM|+|PN|)min=2×3-2=4,
故选A.
点评:本题考查圆锥曲线的性质和应用,解题时要认真审题,仔细解答,注意公式的合理运用.

练习册系列答案
 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目
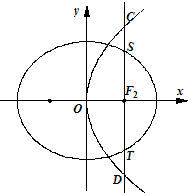 如图,椭圆E:
如图,椭圆E: