题目内容
(2012•青岛一模)已知点M在椭圆D:
+
=1(a>b>0)上,以M为圆心的圆与x轴相切于椭圆的右焦点,若圆M与y轴相交于A,B两点,且△ABM是边长为
的正三角形.
(Ⅰ)求椭圆D的方程;
(Ⅱ)设P是椭圆D上的一点,过点P的直线l交x轴于点F(-1,0),交y轴于点Q,若
=2
,求直线l的斜率;
(Ⅲ)过点G(0,-2)作直线GK与椭圆N:
+
=1左半部分交于H,K两点,又过椭圆N的右焦点F1做平行于HK的直线交椭圆N于R,S两点,试判断满足|GH|•|GK|=3|RF1|•|F1S|的直线GK是否存在?请说明理由.
| x2 |
| a2 |
| y2 |
| b2 |
2
| ||
| 3 |
(Ⅰ)求椭圆D的方程;
(Ⅱ)设P是椭圆D上的一点,过点P的直线l交x轴于点F(-1,0),交y轴于点Q,若
| QP |
| PF |
(Ⅲ)过点G(0,-2)作直线GK与椭圆N:
| 3x2 |
| a2 |
| 4y2 |
| b2 |
分析:(Ⅰ)先确定M的坐标,代入椭圆方程,再利用a2-b2=c2,求出几何量,即可求椭圆D的方程;
(Ⅱ)设出过点P的直线l,利用
=2
,求得P的坐标,代入椭圆方程,即可求直线l的斜率;
(Ⅲ)设直线方程与椭圆方程联立,利用韦达定理,结合|GH|•|GK|=3|RF1|•|F1S|,即可求得结论.
(Ⅱ)设出过点P的直线l,利用
| QP |
| PF |
(Ⅲ)设直线方程与椭圆方程联立,利用韦达定理,结合|GH|•|GK|=3|RF1|•|F1S|,即可求得结论.
解答:解:(Ⅰ)因为△ABM是边长为
的正三角形
所以圆M的半径r=
,M到y轴的距离为d=
r=
,即椭圆的半焦距c=d=
此时点M的坐标为(
,
)…(2分)
因为点M在椭圆D:
+
=1(a>b>0)上
所以
+
=1
又a2-b2=c2=2
解得:a2=6,b2=4
所求椭圆D的方程为
+
=1…(4分)
(Ⅱ)由题意可知直线l的斜率存在,设直线斜率为k
直线l的方程为y=k(x+1),则有Q(0,k)
设P(x1,y1),由于P、Q、F三点共线,且
=2
根据题意得(x1,y1-k)=2(-x1-1,-y1),解得
…(6分)
又P在椭圆D上,故
+
=1
解得k=±
综上,直线l的斜率为k=±
.…(8分)
(Ⅲ)由(Ⅰ)得:椭圆N的方程为
+y2=1…①,
由于F1(1,0),设直线GK的方程为y=kx-2(k<0)…②,
则直线RS的方程为y=k(x-1)(k<0)…③
设H(x3,y3),K(x4,y4)
联立①②消元得:(1+2k2)x2-8kx+6=0,所以x3x4=
所以|GH|•|GK|=
•
=
•
=
…(10分)
设R(x5,y5),S(x6,y6)
联立①③消元得:(1+2k2)x2-4k2x+2k2-2=0
所以x5+x6=
,x5x6=
y5y6=k2[x5x6-(x5+x6)+1]=
3|RF1|•|F1S|=3
•
=3
•
=
…(13分)
由
=
,化简得:k2+1=0,显然无解,
所以满足|GH|•|GK|=3|RF1|•|F1S|的直线GK不存在.…(14分)
2
| ||
| 3 |
所以圆M的半径r=
2
| ||
| 3 |
| ||
| 2 |
| 2 |
| 2 |
此时点M的坐标为(
| 2 |
2
| ||
| 3 |
因为点M在椭圆D:
| x2 |
| a2 |
| y2 |
| b2 |
所以
(
| ||
| a2 |
(
| ||||
| b2 |
又a2-b2=c2=2
解得:a2=6,b2=4
所求椭圆D的方程为
| x2 |
| 6 |
| y2 |
| 4 |
(Ⅱ)由题意可知直线l的斜率存在,设直线斜率为k
直线l的方程为y=k(x+1),则有Q(0,k)
设P(x1,y1),由于P、Q、F三点共线,且
| QP |
| PF |
根据题意得(x1,y1-k)=2(-x1-1,-y1),解得
|
又P在椭圆D上,故
(-
| ||
| 6 |
(
| ||
| 4 |
解得k=±
10
| ||
| 3 |
综上,直线l的斜率为k=±
10
| ||
| 3 |
(Ⅲ)由(Ⅰ)得:椭圆N的方程为
| x2 |
| 2 |
由于F1(1,0),设直线GK的方程为y=kx-2(k<0)…②,
则直线RS的方程为y=k(x-1)(k<0)…③
设H(x3,y3),K(x4,y4)
联立①②消元得:(1+2k2)x2-8kx+6=0,所以x3x4=
| 6 |
| 1+2k2 |
所以|GH|•|GK|=
|
|
|
|
| 6(1+k2) |
| 1+2k2 |
设R(x5,y5),S(x6,y6)
联立①③消元得:(1+2k2)x2-4k2x+2k2-2=0
所以x5+x6=
| 4k2 |
| 1+2k2 |
| 2(k2-1) |
| 1+2k2 |
| -k2 |
| 1+2k2 |
(x5-1)2+
|
(x6-1)2+
|
|
|
| 3(1+k2) |
| 1+2k2 |
由
| 6(1+k2) |
| 1+2k2 |
| 3(1+k2) |
| 1+2k2 |
所以满足|GH|•|GK|=3|RF1|•|F1S|的直线GK不存在.…(14分)
点评:本题考查椭圆的标准方程,考查向量知识的运用,考查直线与椭圆的位置关系,考查韦达定理的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
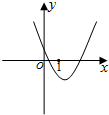 (2012•青岛一模)已知a>b,函数f(x)=(x-a)(x-b)的图象如图所示,则函数g(x)=loga(x+b)的图象可能为
(2012•青岛一模)已知a>b,函数f(x)=(x-a)(x-b)的图象如图所示,则函数g(x)=loga(x+b)的图象可能为